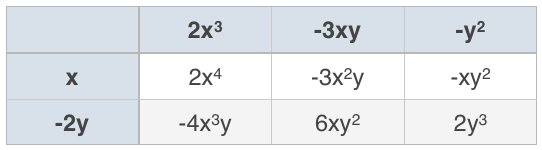How to multiply multivariable polynomials
Paying attention to like terms
Multiplying multivariable polynomials (polynomials with two or more different variables) is very similar to multiplying single-variable polynomials (those that have just one variable). You’ll just need to be careful about combining like terms. In the case of a multivariable polynomial, two terms aren’t “like terms” unless each variable has the same exponent in both of them.
For example, ???3x^2y^3??? and ???-5x^2y^3??? are like terms: In both terms, the variable ???x??? has an exponent of ???2??? and the variable ???y??? has an exponent of ???3???. However, ???-9x^2y??? and ???8xy??? are not like terms: In ???-9x^2y??? the variable ???x??? has an exponent of ???2???, but in ???8xy??? the variable ???x??? has an exponent of ???1???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Here are some reminders about multiplying polynomials.
FOIL
FOIL is a way to help you remember to multiply each term in the first set of parentheses by each term in the second set of parentheses. FOIL stands for Firsts, Outsides, Insides, Lasts, which is the order of the four terms in the result of the multiplication; it also indicates which terms in the given binomials are multiplied to produce each term in the result.
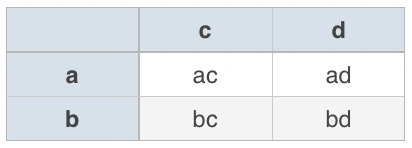
Chart
The example below shows binomial multiplication (two terms by two terms), but a chart can be used when multiplying by more than two terms as well.
???ac+ad+bc+bd???
Multiplying multivariable polynomials step-by-step
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
Multiplying a multivariable binomial by a multivariable trinomial
Let’s look at a couple of examples where we multiply multivariable polynomials.
Example
Simplify the expression.
???(x-2y)(2x^3-3xy-y^2)???
A chart will be useful to make sure we distribute every term in the first set of parentheses across all the terms in the second set of parentheses.
???2x^4-3x^2y-xy^2-4x^3y+6xy^2+2y^3???
Next, we’ll rearrange the terms in descending order of powers of ???x??? (a common practice when dealing with multivariable polynomials).
???2x^4-4x^3y-3x^2y-xy^2+6xy^2+2y^3???
Now we’ll group like terms together, and then combine like terms.
???2x^4-4x^3y-3x^2y+(-xy^2+6xy^2)+2y^3???
???2x^4-4x^3y-3x^2y+5xy^2+2y^3???
Find individual terms by multiplying the polynomials, then group together like terms, then combine like terms to simplify
Let’s try another example of multiplying multivariable polynomials.
Example
Simplify the expression.
???(2x+3y)(x-y)+(x+y)(4x-2y)???
Multiply the first pair of binomials by using either a chart or FOIL.
???2x^2-2xy+3xy-3y^2+(x+y)(4x-2y)???
Combine like terms.
???2x^2+xy-3y^2+(x+y)(4x-2y)???
Multiply the other pair of binomials by using either a chart or FOIL.
???2x^2+xy-3y^2+4x^2-2xy+4xy-2y^2???
Group like terms together, and then combine like terms.
???(2x^2+4x^2)+(xy-2xy+4xy)+(-3y^2-2y^2)???
???6x^2+3xy-5y^2???