Using translation vectors to transform figures
Translation vectors translate a figure from one place to another
In this lesson we’ll look at how to use translation vectors to translate a figure.
A translation vector is a type of transformation that moves a figure in the coordinate plane from one location to another. In other words, a translation vector can be thought of as a slide with no rotating. The slide won’t change the shape or size of the figure, and with no rotation, the orientation won’t change either.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The translation vector can be drawn on the coordinate grid or written as ???\vec{v}=\langle a,b\rangle???. For example, a translation vector that moves a figure ???3??? units right and ???2??? units down can be represented mathematically as ???\vec{v}=\langle3,-2\rangle???, or graphically as
It doesn’t matter where the vector is positioned in the plane. In this figure, the vector starts at ???(1,1)??? and ends at ???(4,-1)???. But the initial point and terminal point of the vector are irrelevant. What matters is the length of the vector and the direction in which it points, so all you have to look at is how many units the vector moves in the ???y???-direction and how many units the vector moves in the ???x???-direction.
Using translation vectors to transform figures in the plane
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
How to use a translation vector to move a triangle in the xy-plane
Example
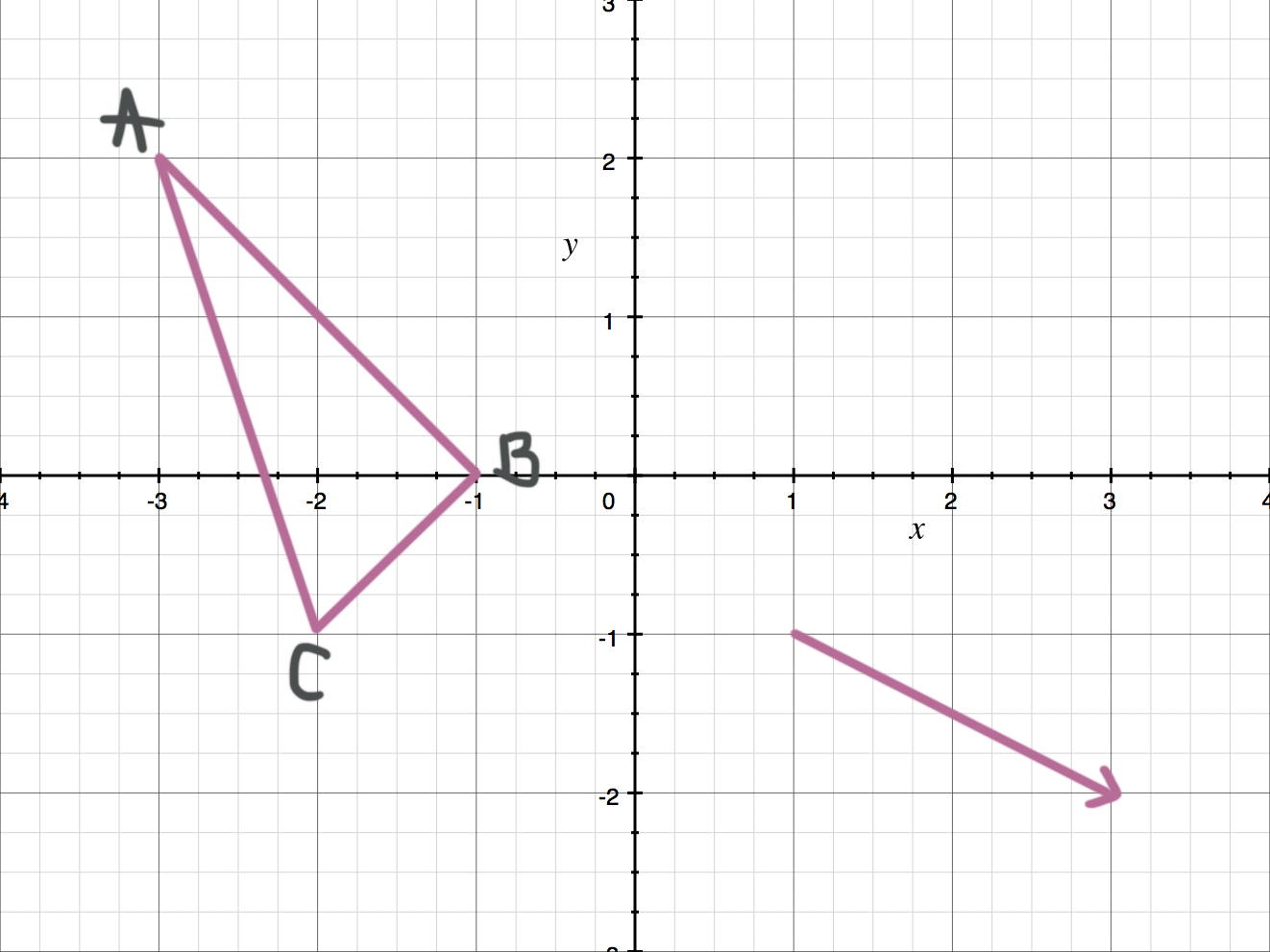
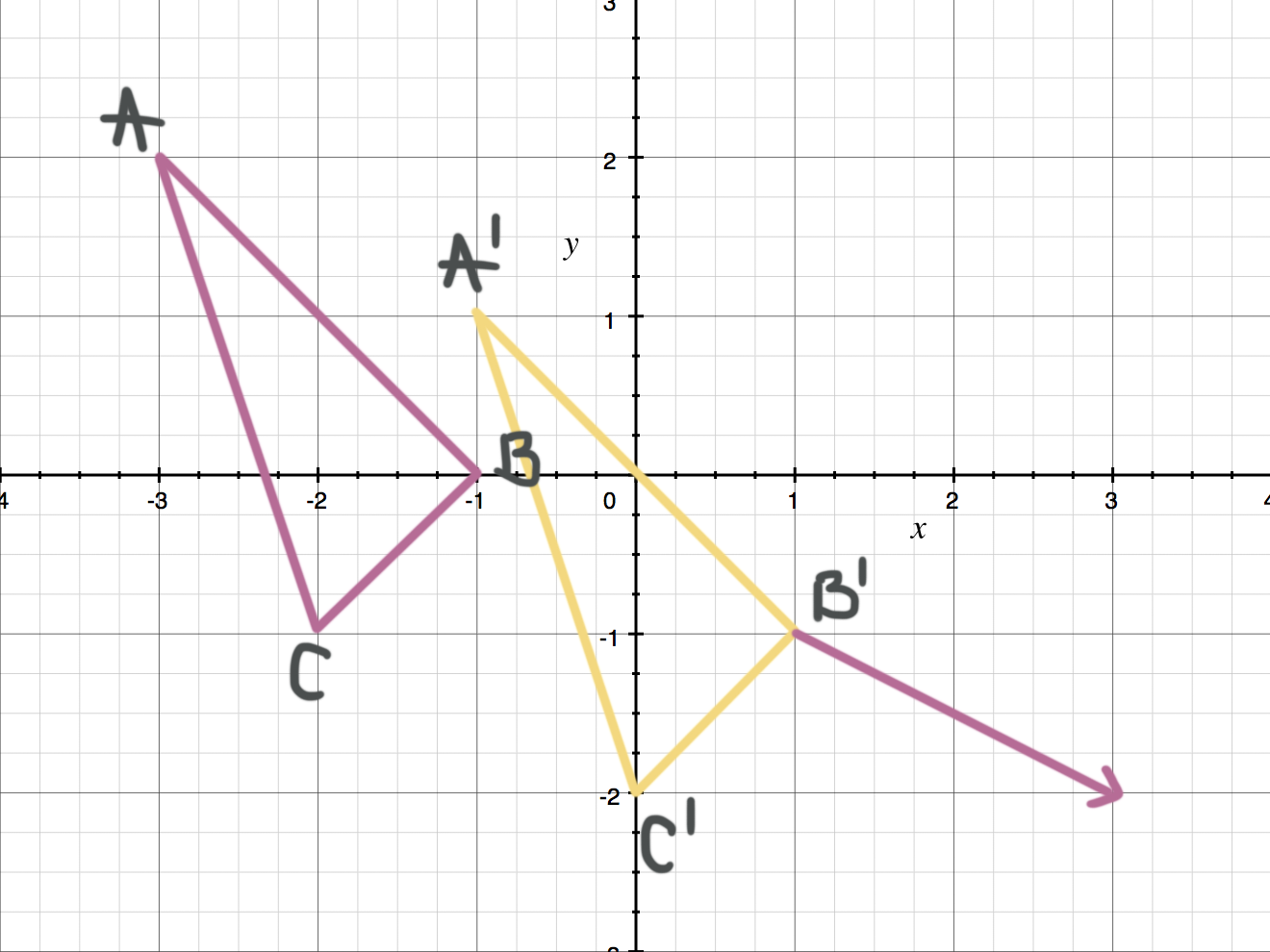
Use the translation vector shown to find the coordinates of triangle ???A'B'C'???.
The vector indicates a translation of ???2??? units to the right and ???1??? unit down. We can therefore add ???2??? to all of the ???x???-values and subtract ???1??? from all of the ???y???-values to find the vertices of the image.
First let’s write down the coordinates of the pre-image, triangle ???ABC???.
???A=(-3,2)???
???B=(-1,0)???
???C=(-2,-1)???
Now we can make the calculations to translate each vertex.
???A'=(-3+2,2-1)=(-1,1)???
???B'=(-1+2,0-1)=(1,-1)???
???C'=(-2+2,-1-1)=(0,-2)???
The image after the translation is
the initial point and terminal point of the Translation vector are irrelevant. What matters is the length of the vector and the direction in which it points.
Finding the coordinates of the image, given the pre-image and the translation vector
Example
Triangle ???ABC??? is a pre-image with its vertices at ???A=(-5,5)???, ???B=(-2,5)???, and ???C=(-3,0)???. If the triangle is translated by ???\vec{v}=\langle -5,-6\rangle???, what are the coordinates of the image?
The translation vector ???\vec{v}=\langle -5,-6\rangle??? means each point is being moved ???5??? units to the left and ???6??? units down. So from each vertex, we’ll subtract ???5??? from each ???x???-value and subtract ???6??? from each ???y???-value.
Then the vertices of the image are
???A'=(-5-5,5-6)=(-10,-1)???
???B'=(-2-5,5-6)=(-7,-1)???
???C'=(-3-5,0-6)=(-8,-6)???