Pythagorean inequalities for classifying triangles
Classifying triangles using Pythagorean inequalities
In this lesson we’ll look at different types of triangles and how to use Pythagorean inequalities to determine what kind of triangle we have based on their angle measures and side lengths.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Types of triangles by angle sizes
Acute triangle
All of the angles are smaller than ???90^\circ???
???m\angle A=79^\circ???
???m\angle B=45^\circ???
???m\angle C=56^\circ???
Right triangle
The triangle has exactly one right angle
???m\angle A=28^\circ???
???m\angle B=90^\circ???
???m\angle C=62^\circ???
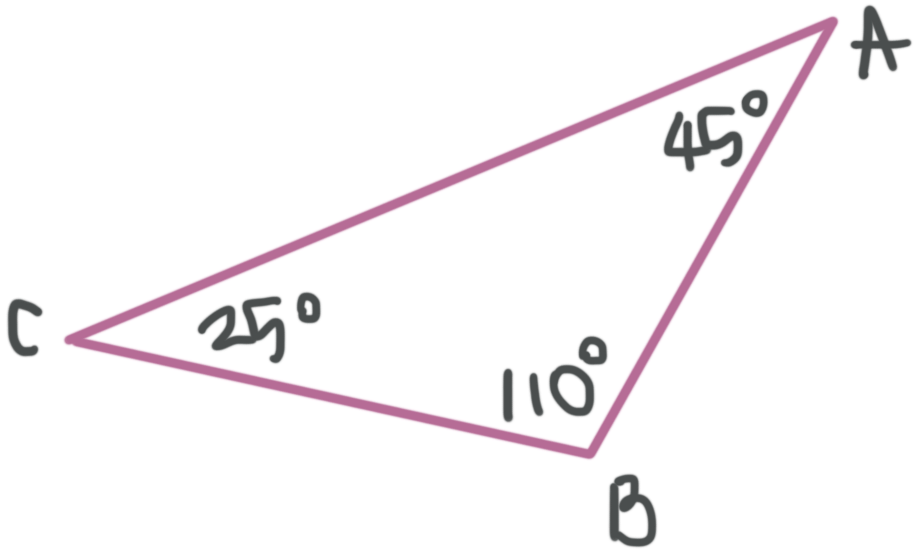
Obtuse triangle
The triangle has one angle greater than ???90^\circ???
???m\angle A=45^\circ???
???m\angle B=110^\circ???
???m\angle C=25^\circ???
Pythagorean inequalities
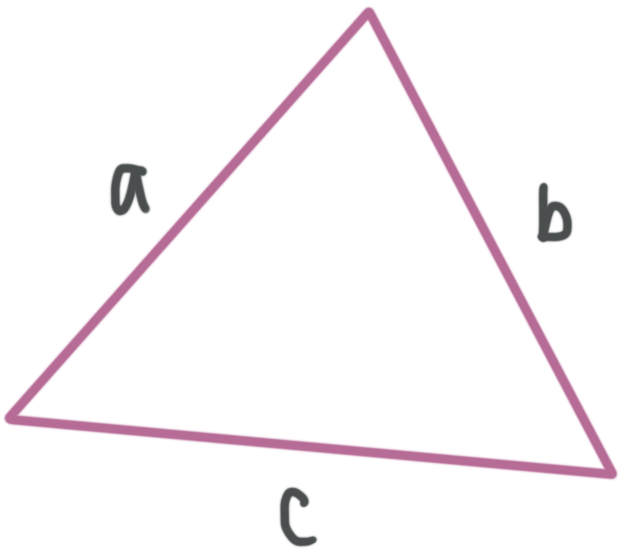
There is a relationship between the length of the two shortest sides of a triangle and the length of its longest side. If the triangle is not a right triangle, then the relationship is an inequality. Just like in the Pythagorean Theorem, we call the short sides ???a??? and ???b??? and the long side ???c???.
Acute triangle
???a^2+b^2>c^2???
Right triangle
???a^2+b^2=c^2???
Obtuse triangle
???a^2+b^2<c^2???
Angles and sides in triangles
One thing to remember about triangles is that the smallest angle is always opposite the shortest side and the biggest angle is always opposite the longest side. Sometimes this can help you when you think through Pythagorean inequality problems.
How to set up Pythagorean inequalities using the triangle’s side lengths
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Classify the triangle as acute, obtuse, or right
Example
Classify the triangle with sides ???10\text{ in}???, ???5\text{ in}???, and ???9\text{ in}??? as acute, obtuse or right.
Use Pythagorean inequalities to classify the triangles. The two shortest sides are ???a??? and ???b??? and the longest side is ???c???, so we can say
???a=5\text{ in}???
???b=9\text{ in}???
???c=10\text{ in}???
Let’s see how ???{{a}^{2}}+{{b}^{2}}??? compares with ???c^2???.
???{{a}^{2}}+{{b}^{2}}\ \ ?\ \ c^2???
???{{5}^{2}}+{{9}^{2}}\ \ ?\ \ {{10}^{2}}???
???25+81\ \ ?\ \ 100???
???106\ \ ?\ \ 100???
Because ???{{a}^{2}}+{{b}^{2}}>{{c}^{2}}???, this is an acute triangle.
The relationship between a triangle’s side lengths, given by a pythagorean inequality, tells you whether the triangle is acute, right, or obtuse
Example
Classify the triangle with sides ???9\text{ in}???, ???7\ \text{in}???, and ???12\text{ in}??? as acute, obtuse or right.
Use Pythagorean inequalities to classify the triangles. The two shortest sides are ???a??? and ???b??? and the longest side is ???c???, so we can say
???a=7\text{ in}???
???b=9\text{ in}???
???c=12\text{ in}???
Let’s see how ???{{a}^{2}}+{{b}^{2}}??? compares with ???c^2???.
???{{a}^{2}}+{{b}^{2}}\ \ ?\ \ {{c}^{2}}???
???{{7}^{2}}+{{9}^{2}}\ \ ?\ \ {{12}^{2}}???
???49+81\ \ ?\ \ 144???
???130\ \ ?\ \ 144???
???130<144???
Because ???{{a}^{2}}+{{b}^{2}}<{{c}^{2}}???, this is an obtuse triangle.
Let’s try one with a bit more reasoning involved.
Finding the side length that will make the triangle obtuse
Example
A triangle has sides ???13\text{ in}??? and ???12 \text{ in}???. If the remaining side is the longest side, what is the smallest integer value it can take that would still keep the triangle obtuse?
For a triangle to be obtuse, its sides need to satisfy the inequality ???{{a}^{2}}+{{b}^{2}}<{{c}^{2}}???. We want to find the largest perfect square that’s bigger than ???{{a}^{2}}+{{b}^{2}}???.
We can set ???a=13\text{ in}??? and ???b=12\text{ in}???, so we have
???13^2+12^2???
???169+144???
???313???
We want ???313??? to be less than ???c^2???, so let’s take the square root of ???313??? and round up to the next integer.
???\sqrt{313}\approx 17.691???
This value rounds up to ???18???, so ???{{c}^{2}}={{18}^{2}}=324???, and the smallest integer side that makes the triangle obtuse is ???18\text{ in}???.