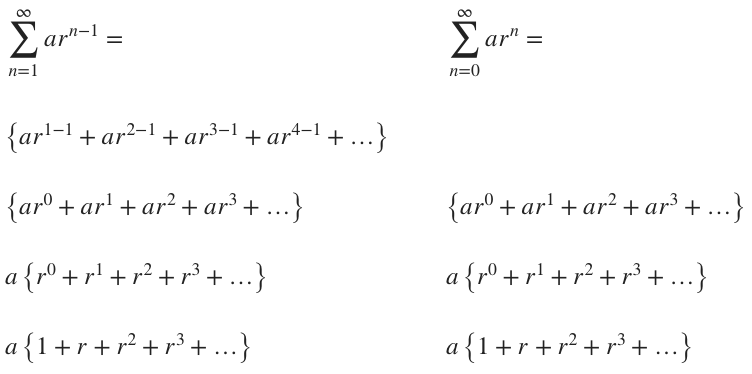Geometric series test to figure out convergence
The geometric series test determines the convergence of a geometric series
Before we can learn how to determine the convergence or divergence of a geometric series, we have to define a geometric series.
The general form of a geometric series is ???ar^{n-1}??? when the index of ???n??? begins at ???n=1???. Therefore, the sum of a convergent geometric series is given by
???\sum^{\infty}_{n=1}ar^{n-1}???
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Sometimes you’ll come across a geometric series with an index shift, where ???n??? starts at ???n=0??? instead of ???n=1???. In that case, the standard form of the geometric series is ???ar^n???, and if it’s convergent, its sum is given by
???\sum^{\infty}_{n=0}ar^n???
Both of these are valid geometric series. The important thing is that the exponent on ???r??? matches the index. So, if the index starts at ???n=1???, we want to make sure we have ???r^{n-1}???. If the index begins at ???n=0???, we want to have ???r^n???.
If we look at the expanded forms of both of these series by calculating the first few terms (???n=1???, ???n=2???, ???n=3??? and ???n=4???, ...), we’ll see that they’re identical.
Which means that, regardless of the kind of geometric series we start with, ???ar^{n-1}??? with ???n=1??? or ???ar^n??? with ???n=0???, we can find the values of ???a??? and ???r??? in the same way: by expanding the series through its first few terms and then factoring out the ???a???. Then ???a??? will be the coefficient we factored out of the series, and ???r??? will be the second term in the series, the term immediately following the ???1???.
???\sum^{\infty}_{n=1}ar^{n-1}=a\left\{1+r+r^2+r^3+...\right\}???
???\ \sum^{\infty}_{n=0}ar^n=a\left\{1+r+r^2+r^3+...\right\}???
Sometimes we won’t even need to expand the series. If we can just make the form of the series match one of the standard forms of a geometric series given above, then we’ll be able to prove that the series is geometric and identify ???a??? and ???r???.
It’s important to be able to find the values of ???a??? and ???r??? because we’ll use ???r??? to say whether or not the geometric series is convergent or divergent. If we find that it’s convergent, then we’ll use ???a??? and ???r??? to find the sum of the series.
Convergence of a geometric series
We can use the value of ???r??? in the geometric series test for convergence to determine whether or not the geometric series converges.
The geometric series test says that
if ???|r|<1??? then the series converges
if ???|r|\ge1??? then the series diverges
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Determining convergence of a geometric series
Example
Show that the series is a geometric series, then use the geometric series test to say whether the series converges or diverges.
???\sum^{\infty}_{n=0}\frac{2^{n-1}}{3^n}???
Since the index starts at ???n=0???, we need to get the series into the form ???ar^n???, which we can do using simple exponent rules.
???\sum^{\infty}_{n=0}\frac{2^{n-1}}{3^n}???
???\sum^{\infty}_{n=0}\frac{2^n2^{-1}}{3^n}???
???\sum^{\infty}_{n=0}2^{-1}\left(\frac{2^n}{3^n}\right)???
???\sum^{\infty}_{n=0}\frac12\left(\frac23\right)^n???
Before we can learn how to determine the convergence or divergence of a geometric series, we have to define a geometric series.
Now that we have the series in the right form, we can say
???\sum^{\infty}_{n=0}ar^n=\sum^{\infty}_{n=0}\frac12\left(\frac23\right)^n??? where
???a=\frac12???
???r=\frac23???
The fact that we’ve been able to put the series in this form and identify values of ???a??? and ???r??? proves that it’s a geometric series. Now we just need to say whether or not the series converges.
Remember that the geometric series test for converges tells us that
if ???|r|<1??? then the series converges
if ???|r|\ge1??? then the series diverges
Since
???\left|\frac23\right|=\frac23<1???
we can say that ???|r|<1??? and therefore that the series converges.