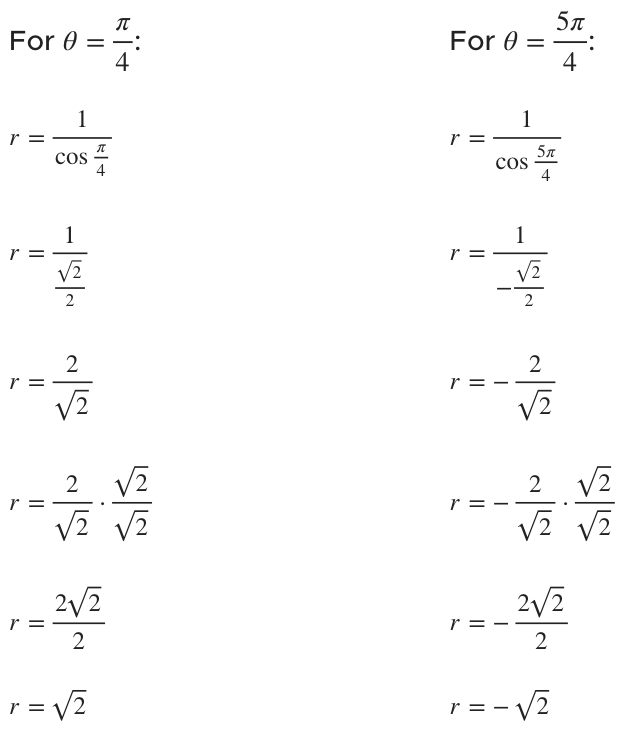Cylindrical coordinates and triple integrals
Cylindrical coordinates as an extension of polar coordinates
Like cartesian (or rectangular) coordinates and polar coordinates, cylindrical coordinates are just another way to describe points in three-dimensional space.
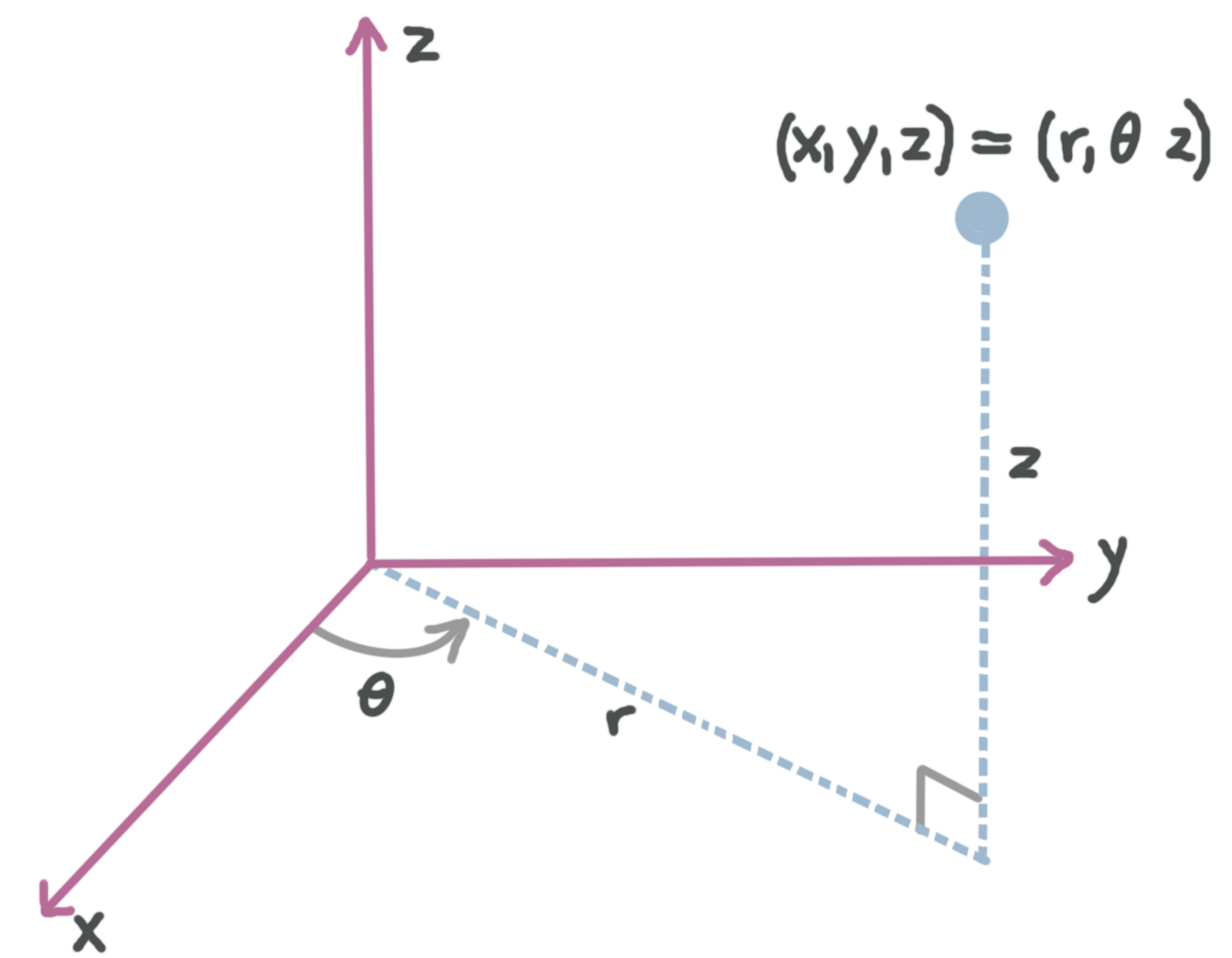
Remember that cylindrical coordinates are exactly the same as polar coordinates, just in three-dimensional space instead of two-dimensional space. Since polar coordinates in 2D are given as ???(r,\theta)???, cylindrical coordinates just require us to add a value for ???z??? to account for 3D space, which means cylindrical coordinates are given as ???(r,\theta,z)???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Rectangular coordinates are given as ???(x,y,z)???
where ???x??? is the distance of ???(x,y,z)??? from the origin along the ???x???-axis
where ???y??? is the distance of ???(x,y,z)??? from the origin along the ???y???-axis
where ???z??? is the distance of ???(x,y,z)??? from the origin along the ???z???-axis
Cylindrical coordinates are given as ???(r,\theta,z)???
where ???r??? is the distance of ???(r,\theta,z)??? from the origin
where ???\theta??? is the angle between ???r??? (the line connecting ???(r,\theta,z)??? to the origin) and the positive direction of the ???x???-axis
where ???z??? is the the distance of ???(r,\theta,z)??? from the origin along the ???z???-axis
To convert between cylindrical coordinates and rectangular coordinates, we use the conversion formulas
???x=r\cos{\theta}???
???y=r\sin{\theta}???
???z=z???
Using cylindrical coordinates to evaluate a triple integral
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
How to convert rectangular coordinates to cylindrical coordinates
Let’s try an example where we convert rectangular coordinates to cylindrical coordinates.
Example
Convert the rectangular coordinate point to a cylindrical coordinate point.
???(1,1,1)???
To convert cylindrical coordinates to rectangular coordinates, we’ll use the formulas
???x=r\cos{\theta}???
???y=r\sin{\theta}???
???z=z???
We’ll plug ???(1,1,1)??? into these conversion formulas.
???1=r\cos{\theta}???
???r=\frac{1}{\cos{\theta}}???
and
???1=r\sin{(\theta)}???
???r=\frac{1}{\sin{\theta}}???
and
???1=z???
Since the first two equations above are equal to ???r???, we can set them equal to each other.
???\frac{1}{\cos{\theta}}=\frac{1}{\sin{\theta}}???
???\cos{\theta}=\sin{\theta}???
???\theta=\frac{\pi}{4},\ \frac{5\pi}{4}???
Since we found two values for ???\theta???, we’ll have two cylindrical coordinate points that can represent the given rectangular coordinate point. We’ll plug our ???\theta??? values into the equation we found for ???r???.
It looks like there are two values for ???r??? in cylindrical coordinates. However, remember that ???r??? represents the radius, or distance from the origin. It doesn’t make sense to say that we’re ???-\sqrt2??? units away from the origin. So we drop that value for ???r??? and only consider the positive ???\sqrt2???.
Putting these values together, we can say that the rectangular coordinate ???(1,1,1)??? is the same as the cylindrical coordinate
???\left(\sqrt{2},\frac{\pi}{4},1\right)???
cylindrical coordinates are exactly the same as polar coordinates, just in three-dimensional space instead of two-dimensional space.
Converting cylindrical coordinates back to rectangular coordinates
Let’s try an example where we convert cylindrical coordinates to rectangular coordinates.
Example
Convert the cylindrical coordinate point to a rectangular coordinate point.
???(2,\pi,3)???
To convert cylindrical coordinates to rectangular coordinates, we’ll use the formulas
???x=r\cos{\theta}???
???y=r\sin{\theta}???
???z=z???
Remember, cylindrical coordinates are given in the form ???(r,\theta,z)???, which means that
???r=2???
???\theta=\pi???
???z=3???
We’ll plug these values into our conversion formulas to find ???(x,y,z)???.
???x=2\cos{\pi}???
???x=2(-1)???
???x=-2???
and
???y=2\sin{\pi}???
???y=2(0)???
???y=0???
and
???z=3???
Putting these values together, we can say that the cylindrical coordinate ???(2,\pi,3)??? is the same as the rectangular coordinate ???(-2,0,3)???.