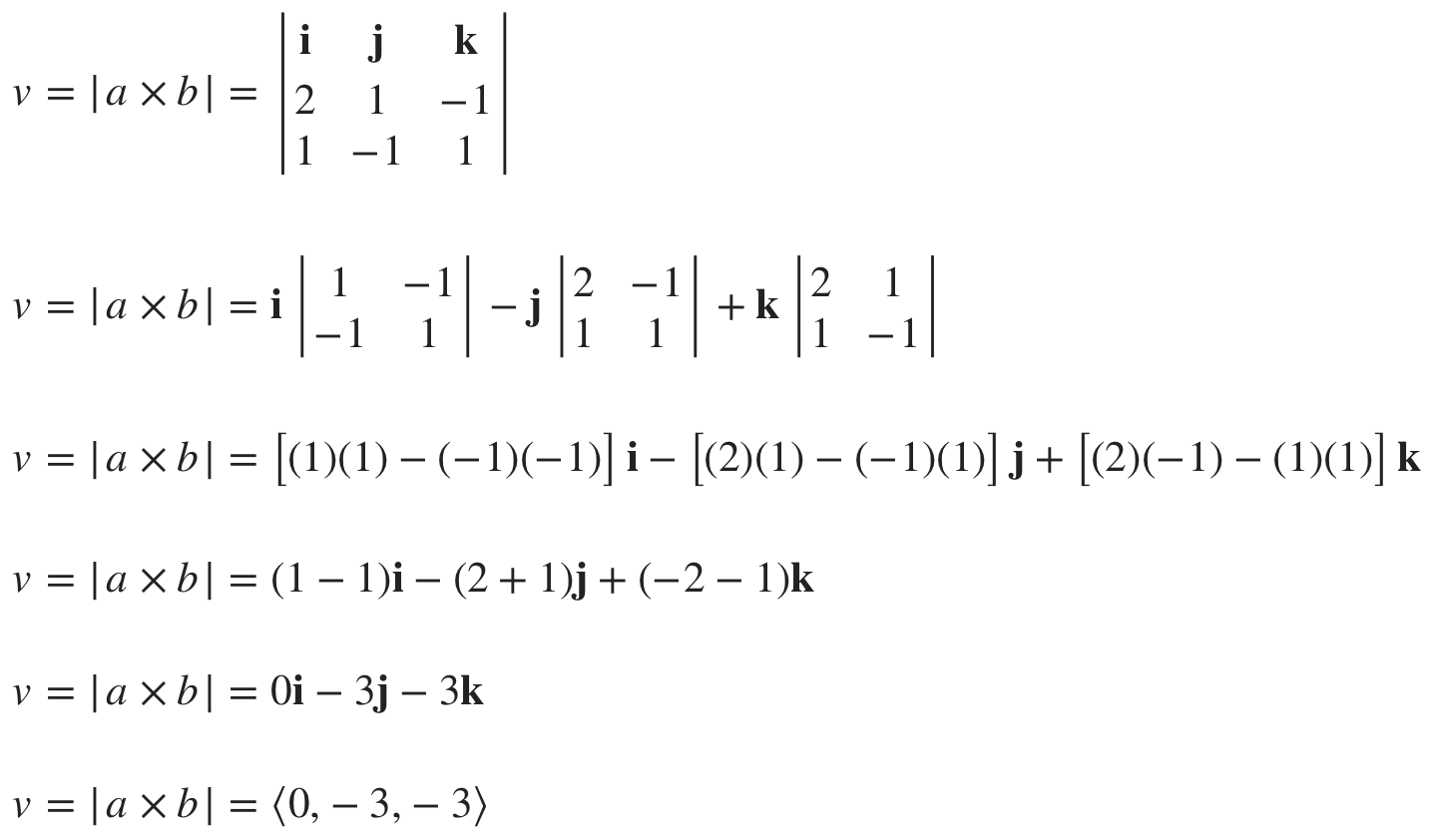Symmetric equations for the line of intersection of two planes
Two intersecting planes always form a line
If two planes intersect each other, the intersection will always be a line.
The vector equation for the line of intersection is given by
???r=r_0+tv???
where ???r_0??? is a point on the line and ???v??? is the vector result of the cross product of the normal vectors of the two planes.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The symmetric equations for the line of intersection are given by
???\frac{x-a_1}{v_1}=\frac{y-a_2}{v_2}=\frac{z-a_3}{v_3}???
where ???a(a_1,a_2,a_3)??? are the coordinates from a point on the line of intersection and ???v_1???, ???v_2??? and ???v_3??? come from the cross product of the normal vectors to the given planes.
Video walkthrough of how to find the symmetric equations for the intersection line
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Step-by-step example of finding the intersection line as a symmetric equation
Example
Find the parametric equations for the line of intersection of the planes.
???2x+y-z=3???
???x-y+z=3???
We need to find the vector equation of the line of intersection. In order to get it, we’ll need to first find ???v???, the cross product of the normal vectors of the given planes.
The normal vectors for the planes are
???a\langle2,1,-1\rangle??? for the plane ???2x+y-z=3???
???b\langle1,-1,1\rangle??? for the plane ???x-y+z=3???
The cross product of the normal vectors is
We also need a point of on the line of intersection. To get it, we’ll use the equations of the given planes as a system of linear equations. If we set ???z=0??? in both equation, we get
???2x+y-z=3???
???2x+y-0=3???
???2x+y=3???
and
???x-y+z=3???
???x-y+0=3???
???x-y=3???
Now we’ll add the equations together.
???(2x+x)+(y-y)=3+3???
???3x+0=6???
???x=2???
Plugging ???x=2??? back into ???x-y=3???, we get
???2-y=3???
???-y=1???
???y=-1???
To find the symmetric equations, you’ll need the cross product of the normal vectors of the two planes, as well as a point on the line of intersection
Putting these values together, the point on the line of intersection is
???(2,-1,0)???
???r_0=2\bold i-\bold j+0\bold k???
???r_0=\langle 2,-1,0\rangle???
With the cross product of the normal vectors and the point on the line of intersection, we can plug into the formula for the symmetric equations, and get
???x-2???, ???\frac{y-(-1)}{-3}=\frac{z-0}{-3}???
???x-2???, ???-\frac{y+1}{3}=-\frac{z}{3}???
Remember, since the direction number for ???x??? from the cross product ???v=|a\times b|=\langle0,-3,-3\rangle??? is ???0???, we have to pull the symmetric equation for ???x??? away from the other two and keep it by itself so that we don’t have to divide by ???0???.