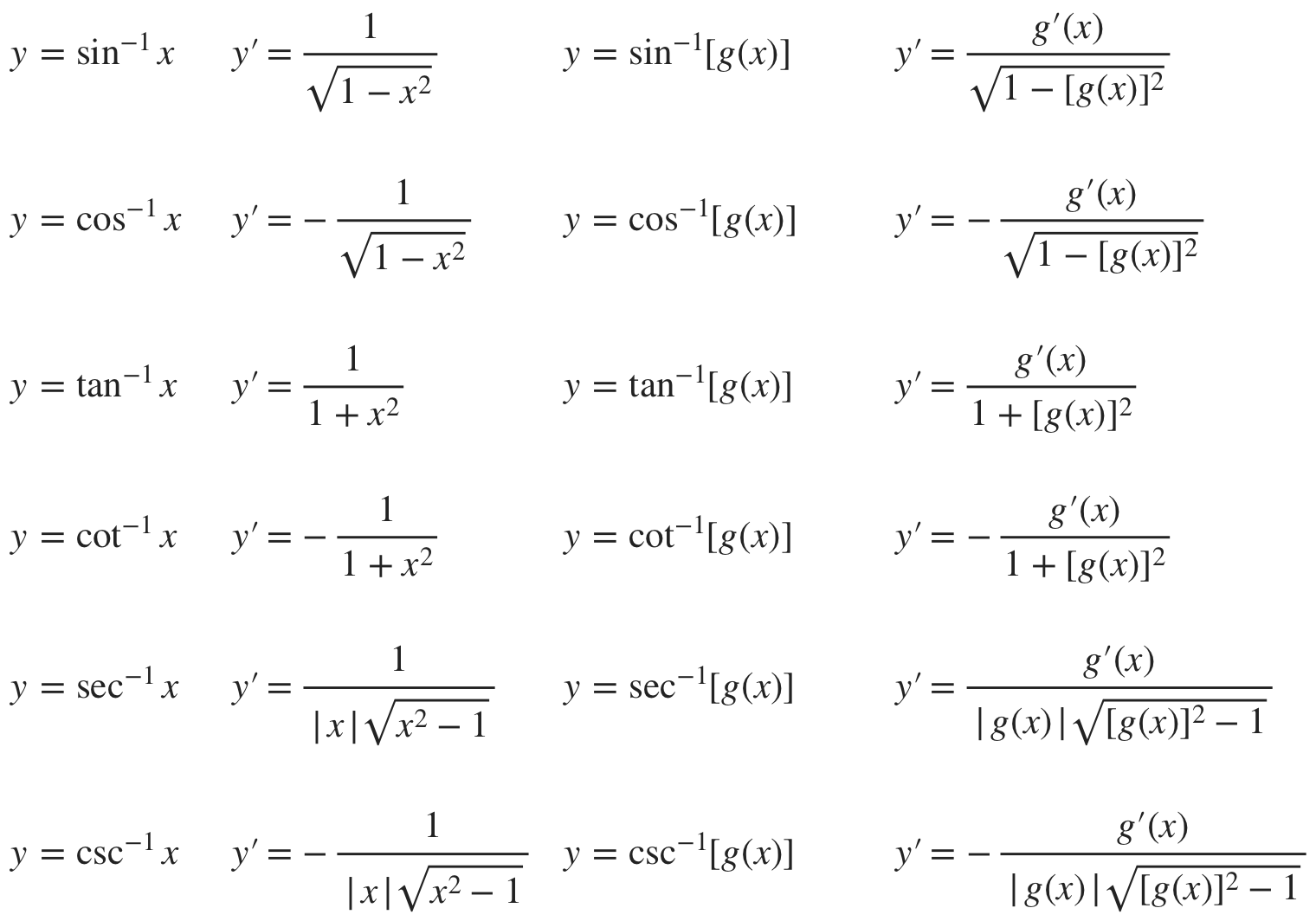Finding inverse trig derivatives
The difference between an inverse function and a -1 exponent
Before we talk about inverse trigonometric functions, let’s review inverse functions in general. If we want to find the inverse of a function, we just replace all the ???x???’s with ???y???’s and all the ???y???’s with ???x???’s. So if we want to find the inverse of ???y=\sin{x}???, we flip the variables and we get ???x=\sin{y}???. Then we solve this equation for ???y??? by taking inverse sine (???\sin^{-1}??? or ???\arcsin???) of both sides, because the ???\sin^{-1}??? and the ???\sin??? will cancel on the right side.
???\sin^{-1}{x}=\sin^{-1}{(\sin{y})}???
???\sin^{-1}{x}=y???
???y=\sin^{-1}{x}??? or ???y=\arcsin{x}???
???\sin^{-1}??? and ???\arcsin??? both indicate the inverse of the ???\sin??? function and can be used interchangeably. Remember that
???x^{-1}=\frac{1}{x}??? but ???\sin^{-1}{x}\neq\frac{1}{\sin{x}}???
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Because some people think incorrectly that the negative exponent rule can be applied to inverse trigonometric functions, others argue that ???\arcsin??? is more clear and should always be used instead of ???\sin^{-1}??? to indicate the inverse trigonometric function. You should use whichever notation you’re comfortable with, unless your professor expects you to use one of them consistently. The fact is, you usually see both of them used, so you should be familiar with both and remember that they mean the same thing.
The first two columns of the chart below show the six inverse trigonometric functions and their derivatives, when the “inside” function is just ???x???. The third and forth columns take chain rule into account and remind us to multiply by the derivative of the inside function.
Video example of the derivative of inverse sine
Video example of the derivative of inverse cotangent
Take the course
Want to learn more about Calculus 1? I have a step-by-step course for that. :)
How to find the derivative of the inverse tangent function
Example
Find the derivative.
???y=7\tan^{-1}\left(4x^3\right)???
Remember, we apply chain rule by first taking the derivative of the inverse trigonometric function (inverse tangent, in this case), leaving the inside function (???4x^3???, in this case) completely untouched, and then we multiply our result by the derivative of the inside function.
???y\prime=7\left[\frac{12x^2}{1+\left(4x^3\right)^2}\right]???
???y\prime=\frac{84x^2}{1+16x^6}???
???y\prime=\frac{84x^2}{16x^6+1}???
To find an inverse trig derivative, just apply the formulas from the derivative table
It’s common to see inverse trigonometric functions mixed into more elaborate functions, so let’s try an example with an inverse trigonometric function occurring as part of a larger function.
How to find the derivative of the inverse secant function
Example
Find the derivative.
???y=2\sec^{-1}\left(x^3\right)-54x^7???
Taking the derivative term by term, using the formulas from our table, and remembering to apply chain rule, we get
???y\prime=2\left[\frac{3x^2}{\left|x^3\right|\sqrt{\left(x^3\right)^2-1}}\right]-378x^6???
???y\prime=\frac{6x^2}{\left|x^3\right|\sqrt{x^6-1}}-378x^6???
Let’s try another more complex example.
An example with the inverse cosine function
Example
Find the derivative.
???y=2x^6-x^3\left[\cos^{-1}(2x)\right]+8\sin{\left(3x^5\right)}???
We’ll need to use product rule for the second term, ???x^3\left[\cos^{-1}(2x)\right]???. Taking the derivative term by term, using the formulas from our table, and remembering to also apply chain rule, we get
???y\prime=12x^5-\left[\left(3x^2\right)\left(\cos^{-1}{(2x)}\right)+\left(x^3\right)\left(-\frac{2}{\sqrt{1-(2x)^2}}\right)\right]+8\cos{\left(3x^5\right)}\left(15x^4\right)???
???y\prime=12x^5-\left[3x^2\cos^{-1}{(2x)}-\frac{2x^3}{\sqrt{1-4x^2}}\right]+120x^4\cos{\left(3x^5\right)}???
???y\prime=12x^5-3x^2\cos^{-1}{(2x)}+\frac{2x^3}{\sqrt{1-4x^2}}+120x^4\cos{\left(3x^5\right)}???
???y\prime=12x^5+120x^4\cos{\left(3x^5\right)}+\frac{2x^3}{\sqrt{1-4x^2}}-3x^2\cos^{-1}{(2x)}???