Similar triangles have corresponding sides and angles
Similar triangles have corresponding angles and corresponding sides
In this lesson we’ll look at the ratios of similar triangles to find out missing information about similar triangle pairs.
Similar triangles
In a pair of similar triangles, corresponding sides are proportional and all three angles are congruent. This means if you know two triangles are similar to one another you can use the information to solve for missing parts.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
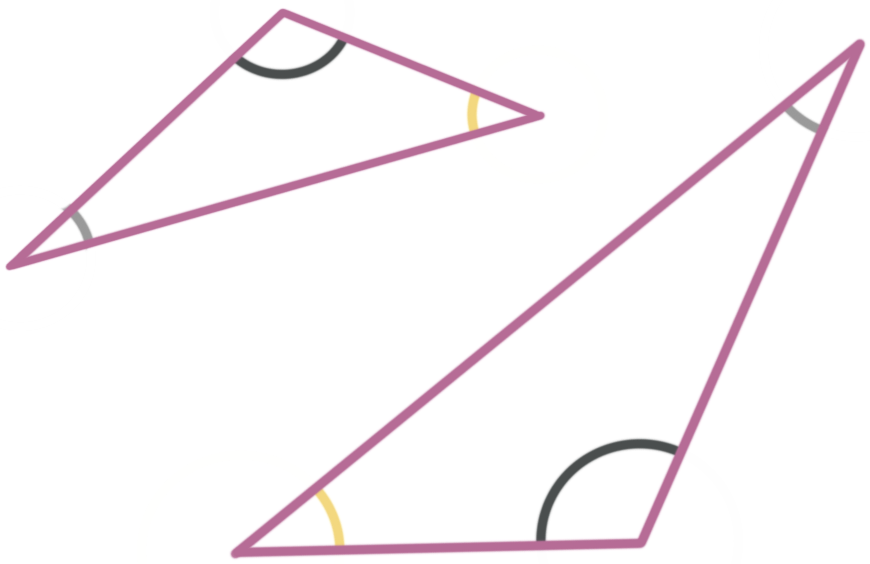
Corresponding angles
In a pair of similar triangles the corresponding angles are the angles with the same measure. In the diagram of similar triangles, the corresponding angles are the same color.
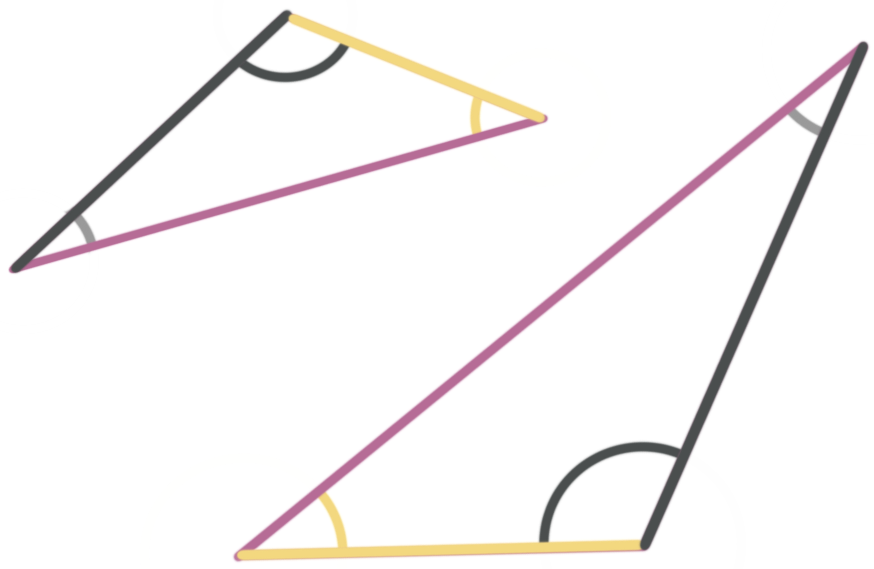
Corresponding sides
In a pair of similar triangles, the corresponding sides are proportional. Corresponding sides touch the same two angle pairs.
When the sides are corresponding it means to go from one triangle to another you can multiply each side by the same number.
In the diagram of similar triangles the corresponding sides are the same color.
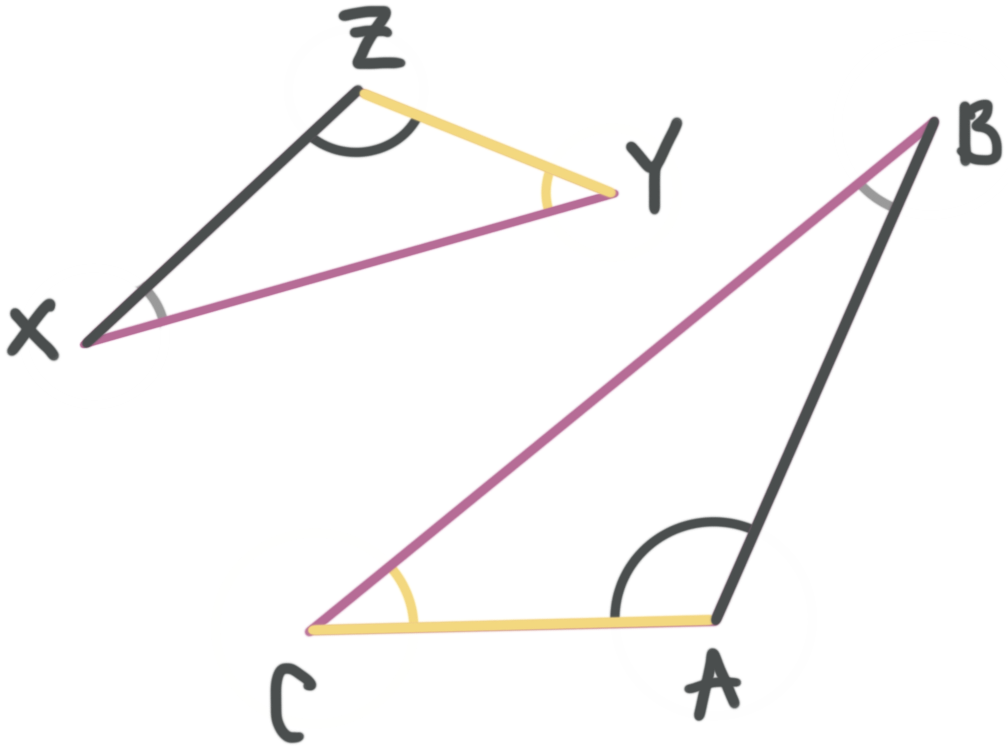
Naming similar triangles
To show two triangles are similar, you use the symbol ???\sim???. You need to match the letters from the first triangle to the angles with the corresponding vertices on the second triangle.
Here we can say that ???\triangle XYZ\sim \triangle BCA???.
When triangles are similar, you can use that fact to solve for the value of angles and sides
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Solving for the variable in two similar triangles
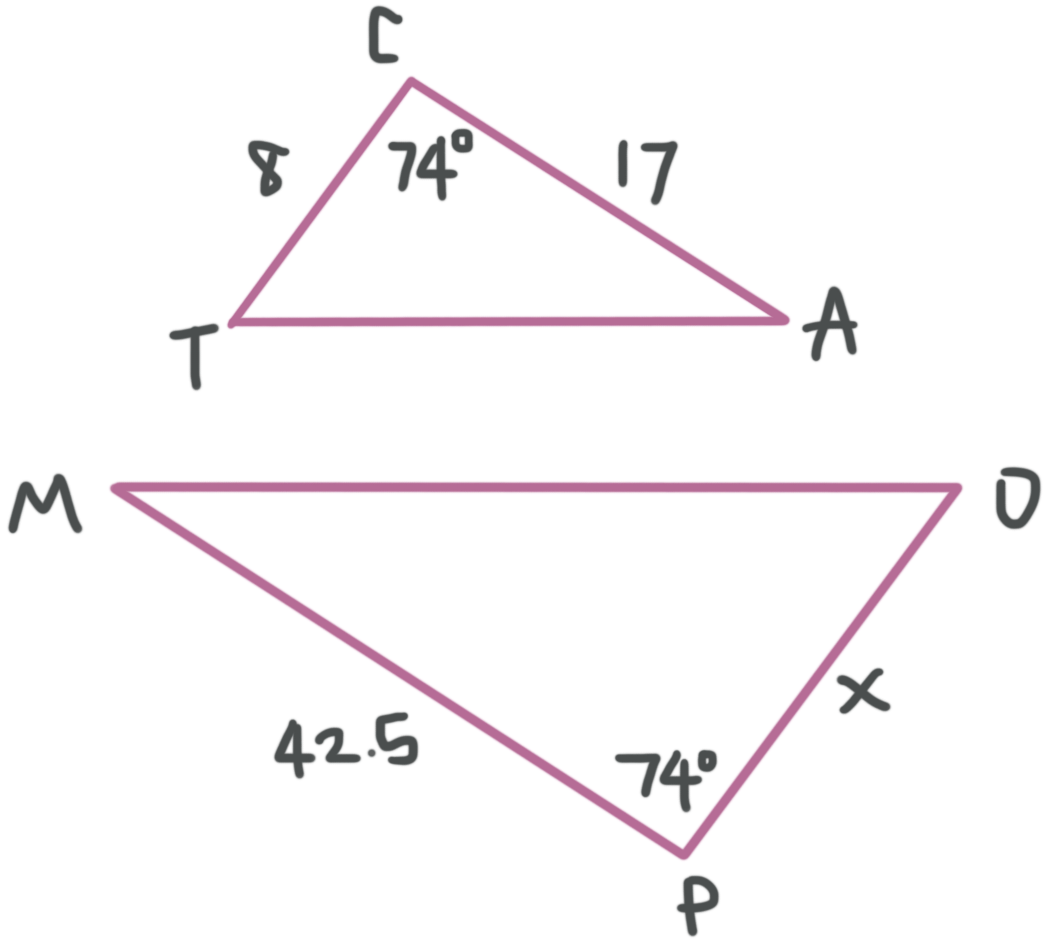
Example
If the two triangles in the diagram are similar, solve for the variable.
In similar triangles, corresponding sides are proportional. In the diagram, ???x??? corresponds to ???8???, and ???42.5??? corresponds to ???17???. So we say
???\frac{x}{8}=\frac{42.5}{17}???
???17x=8(42.5)???
???17x=340???
???x=20???
Corresponding sides touch the same two angle pairs.
How to solve for values in similar triangles
Example
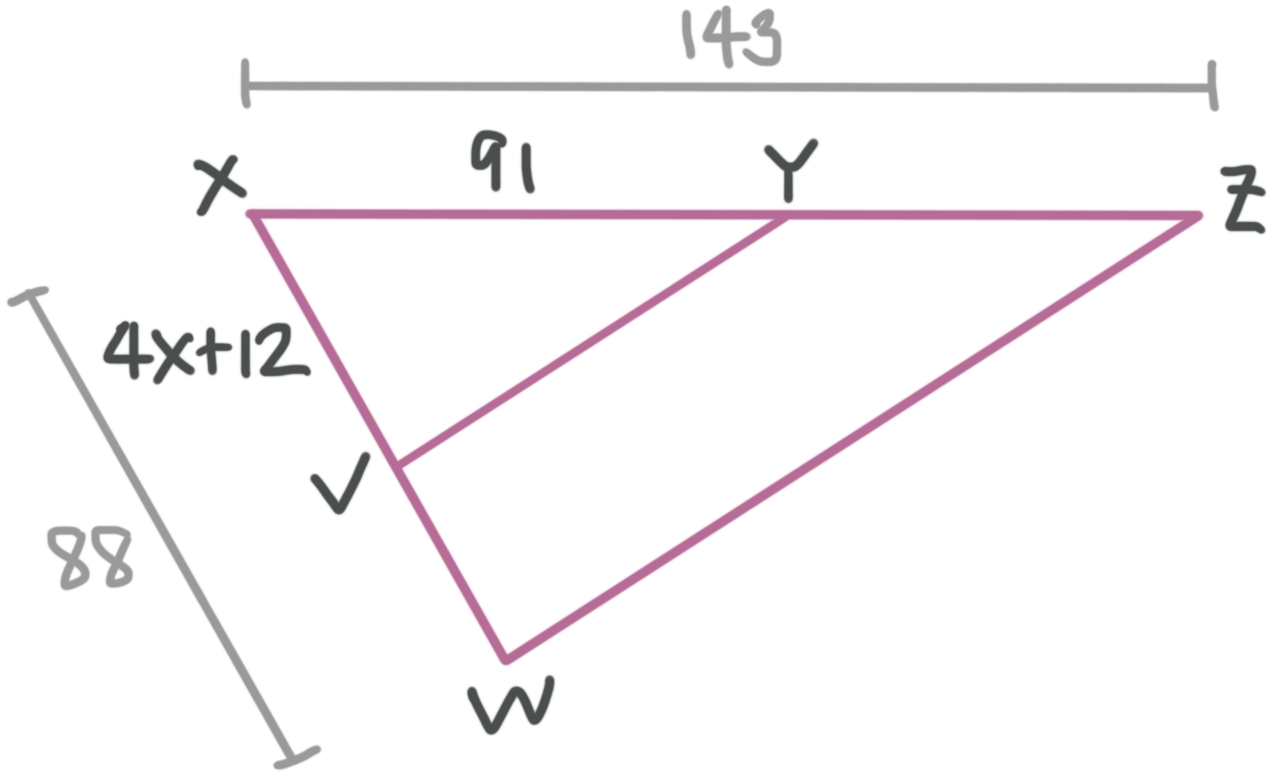
If ???\triangle XVY\sim \triangle XWZ???, solve for ???x???.
In similar triangles, corresponding sides are proportional. In the diagram, ???4x+12??? corresponds to ???88???, and ???91??? corresponds to ???143???.
???\frac{4x+12}{88}=\frac{91}{143}???
???(4x+12)143=91(88)???
???(4x+12)143=8,008???
???\frac{(4x+12)143}{143}=\frac{8,008}{143}???
???4x+12=56???
???4x=44???
???x=11???