Number sets in the real number system
There are more numbers than just the “counting numbers”
When I say the word “numbers,” you probably immediately think about these:
???1,\ 2,\ 3,\ 4,\ 5,\ ...???
or, you might think of these:
???0,\ 1,\ 2,\ 3,\ 4,\ 5,\ ...???
But when most people think about numbers in general, they don’t usually think about the other kinds of numbers that we’ll talk about in this course, like negative numbers, fractions and decimals, or radical numbers.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Without going into too much detail in this lesson, we just want to take this lesson to get a little preview of different kinds of number sets. Since we’ll be covering each of these kinds of numbers later on, right now we really just want to define each of the different number sets.
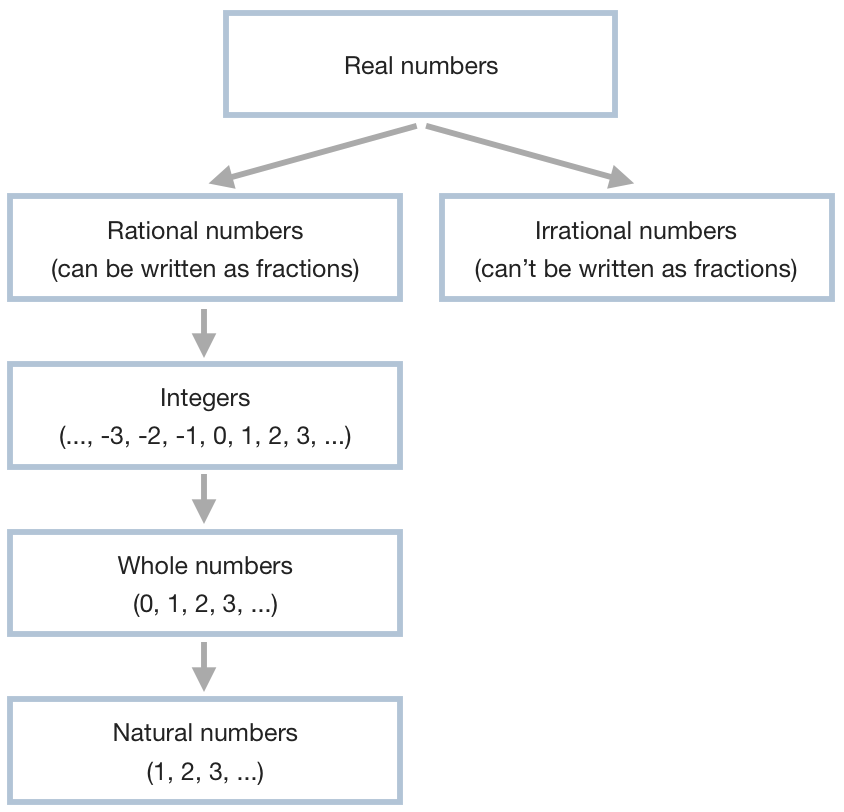
Real numbers
The vast majority of the numbers you’ll use in most math classes are called real numbers, and the whole universe of real numbers is what makes up the Real Number System. Let’s start with a diagram.
Real numbers include rational numbers and irrational numbers. Rational numbers are fractions, which look like this:
???\frac14,\ \frac32,\ -\frac18,\ \frac67,\ -\frac23,\ ...???
Decimal numbers that terminate or repeat are also rational numbers and can look like this:
???- 0.25,\ 0.333,\ 5.7,\ ...???
Irrational numbers are all numbers that can’t be written as a fraction. These are irrational roots like ???\sqrt2??? and decimal numbers like ???\pi??? that go on forever.
???\sqrt2=1.41421356237...???
???\pi=3.14159265359...???
Again, we’ll go into more detail about these later.
Integers are a special kind of rational number. They’re made up of all the numbers you normally think about, like ???0,\ 1,\ 2,\ 3,\ 4,\ 5,\ ...???, plus negative numbers as well. So the set of integers looks like this:
???...\ -5,\ -4,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ ...???
Within the set of integer numbers is a set of numbers that we call whole numbers, which is made up of all positive integers, plus ???0???. So the set of whole numbers is
???0,\ 1,\ 2,\ 3,\ 4,\ 5,\ ...???
And within the set of whole numbers, we define a set called the natural numbers, which is only the set of all positive integers, without ???0???. So the set of natural numbers is
???1,\ 2,\ 3,\ 4,\ 5,\ ...???
We often refer to natural numbers as the “counting numbers,” since ???1,\ 2,\ 3,\ 4,\ 5,\ ...??? is how we learn to count when we’re young.
Hierarchy of number sets in the real number system
Take the course
Want to learn more about Pre-Algebra? I have a step-by-step course for that. :)
Number set symbols
Each of these number sets is indicated with a symbol. We use the symbol as a short-hand way of referring to the values in the set.
R represents the set of real numbers
Q represents the set of rational numbers
Z represents the set of integers
W represents the set of whole numbers
N represents the set of natural numbers
Because irrational numbers is all real numbers, except all of the rational numbers (which includes rationals, integers, whole numbers and natural numbers), we usually express irrational numbers as R-Q, or R\Q.
R-Q represents the set of irrational numbers
The vast majority of the numbers you’ll use in most math classes are called real numbers, and the whole universe of real numbers is what makes up the Real Number System.
Set notation
Here we’ve talked about number sets, but we can also think about sets of things other than numbers. For example, you could describe the people in a family as
???\text{Family}=\{\text{Father}, \text{Mother}, \text{Sister},\ \text{Brother}\}???
or countries in North America as
???\text{North American countries}=\{\text{Canada}, \text{United States}, \text{Mexico}\}???
We usually use those curly braces to enclose the members of the set. So using the symbols we learned for number sets, in set notation you could write the set of all natural numbers as
???\text{N}=\{1,\ 2,\ 3,\ 4,\ 5,\ ...\}???