Calculating absolute values
The absolute value is just the distance from the origin
The idea of absolute value is really just the idea of “distance from ???0???.” Going back to the idea of a number line,
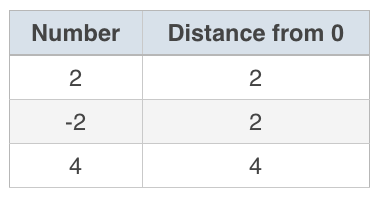
we can say that ???2??? is a distance of two units away from ???0???, but also that ???-2???, the opposite of ???2??? (and on the other side of ???0???), is two units away from ???0???. So both ???2??? and ???-2??? are two units away from ???0???. The number ???4??? is four units away from ???0???, and ???-5??? is five units away from ???0???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
So notice that, if we translate both positive and negative numbers into just their distance from ???0???, we get
Interestingly, all these numbers, whether they started out as positive or negative, become positive numbers when we think only about their distance from ???0???.
In fact, this is exactly what the absolute value operation does for us. It turns each number into its distance from the origin, essentially turning all positive and negative numbers into only positive numbers. (Also, it “turns” ???0??? into ???0???, because the number ???0??? is zero units away from itself.)
We indicate the absolute value of a number by enclosing it in a pair of vertical bars (which we’ll call “absolute value bars”). Here’s an example of what the absolute value operation looks like:
???|-3|???
This means “take the absolute value of ???-3???.” We already know that the absolute value of ???-3??? is ???3???, since ???-3??? is a distance of three units away from ???0???. Here are some more examples:
Finding the absolute value of different positive and negative numbers
Take the course
Want to learn more about Pre-Algebra? I have a step-by-step course for that. :)
Finding the absolute value of a larger expression
We aren't limited to taking the absolute value of just a number. In fact, we can take the absolute value of any mathematical expression (e.g., an expression for addition, subtraction, multiplication, or division, or an expression that includes two or more of those operations), and we enclose the entire expression in a pair of absolute value bars.
While it’s true that the absolute value bars make whatever’s inside them positive (unless the value of the expression is ???0???, in which case it makes the absolute value ???0???), there’s one important thing we need to say. We MUST evaluate the expression inside the absolute value bars before taking the absolute value. As an example, consider
???|-3-4|???
We MUST evaluate the expression inside the absolute value bars before taking the absolute value.
You might be tempted to think that the absolute value operation just takes away the negative sign that goes with the ???3???, and you would probably get ???1??? as the answer:
???|-3-4|???
???|3-4|???
???|-1|???
???1???
But this is wrong, because you would have performed the absolute value operation first, by taking away the first negative sign inside the absolute value bars. What we need to do instead is evaluate the expression inside the absolute value bars first, and THEN take the absolute value. This is how we should solve it:
???|-3-4|???
???|-7|???
???7???
Notice how we first dealt with the subtraction problem inside the absolute value bars, by evaluating ???-3-4??? as ???-7???. Only then, once we had evaluated that expression, did we take the absolute value.