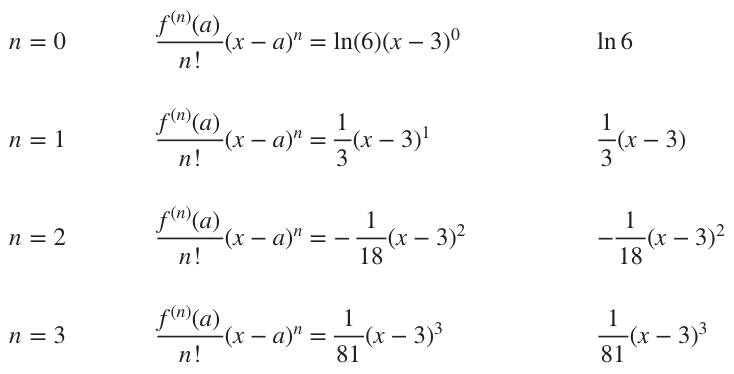Finding radius and interval of convergence of a Taylor series
Start by representing the Taylor series as a power series
Sometimes we’ll be asked for the radius and interval of convergence of a Taylor series. In order to find these things, we’ll first have to find a power series representation for the Taylor series.
Once we have the Taylor series represented as a power series, we’ll identify ???a_n??? and ???a_{n+1}??? and plug them into the limit formula from the ratio test in order to say where the series is convergent.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
How to find the radius and interval of convergence of a Taylor series
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Step-by-step solution for finding the radius and interval of convergence
Example
Using the chart below, find the third-degree Taylor series about ???a=3??? for ???f(x)=\ln(2x)???. Then find the power series representation of the Taylor series, and the radius and interval of convergence.
Taylor series
Since we already have the chart done, the value in the far right column becomes the coefficient on each term in the Taylor polynomial, in the form
???\frac{f^{(n)}(a)}{n!}(x-a)^n???
With the whole chart filled in, we can build each term of the Taylor polynomial.
Putting all of the terms together, we get the third-degree Taylor polynomial.
???\ln{6}+\frac{1}{3}(x-3)-\frac{1}{18}(x-3)^2+\frac{1}{81}(x-3)^3???
Power series representation
We want to find a power series representation for the Taylor series above. The first thing we can see is that the exponent of each ???(x-3)??? is equal to the ???n??? value of that term, which means that
???(x-3)^n???
will be part of the power series representation. The fractional coefficient in front of the ???(x-3)??? terms can be represented by
???\frac{1}{n3^n}???
Finally, we need to deal with the negative sign in front of the ???n=2??? term. If we multiply our terms by
???(-1)^{n+1}???
the ???n=2??? term will be negative and the ???n=1??? and ???n=3??? terms will be positive. Remember, none of these generalizations apply to our ???n=0??? term, so we’ll leave this term outside of the power series representation.
???\ln{6}+\sum^{\infty}_{n=1}\frac{(-1)^{n+1}(x-3)^n}{n3^n}???
Notice the sum starts at ???n=1???, since the ???n=0??? term is not included in the sum.
Radius and interval of convergence
To find the radius of convergence, we’ll identify ???a_n??? and ???a_{n+1}??? using the power series representation we just found.
???a_n=\frac{(-1)^{n+1}(x-3)^n}{n3^n}???
???a_{n+1}=\frac{(-1)^{n+2}(x-3)^{n+1}}{3^{n+1}(n+1)}???
We can plug ???a_n??? and ???a_{n+1}??? into the limit formula from the ratio test.
???L=\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|???
???L=\lim_{n\to\infty}\left|\frac{\frac{(-1)^{n+2}(x-3)^{n+1}}{(n+1)3^{n+1}}}{\frac{(-1)^{n+1}(x-3)^n}{n3^n}}\right|???
???L=\lim_{n\to\infty}\left|\frac{(-1)^{n+2}(x-3)^{n+1}}{(n+1)3^{n+1}}\cdot\frac{n3^n}{(-1)^{n+1}(x-3)^n}\right|???
???L=\lim_{n\to\infty}\left|\frac{(-1)^{n+2}}{(-1)^{n+1}}\cdot\frac{(x-3)^{n+1}}{(x-3)^n}\cdot\frac{n}{n+1}\cdot\frac{3^n}{3^{n+1}}\right|???
???L=\lim_{n\to\infty}\left|(-1)^{n+2-(n+1)}\cdot(x-3)^{n+1-n}\cdot\frac{n}{n+1}\cdot3^{n-(n+1)}\right|???
???L=\lim_{n\to\infty}\left|(-1)^{n+2-n-1}\cdot(x-3)^{n+1-n}\cdot3^{n-n-1}\cdot\frac{n}{n+1}\right|???
???L=\lim_{n\to\infty}\left|(-1)^{1}\cdot(x-3)^{1}\cdot3^{-1}\cdot\frac{n}{n+1}\right|???
???L=\lim_{n\to\infty}\left|-\frac13(x-3)\frac{n}{n+1}\right|???
Since we’re dealing with absolute value, the ???-1??? can be removed.
???L=\lim_{n\to\infty}\left|\frac{n(x-3)}{3(n+1)}\right|???
The limit only effects ???n???, so we can remove the ???(x+3)???.
???L=|x-3|\lim_{n\to\infty}\left|\frac{n}{3(n+1)}\right|???
???L=|x-3|\lim_{n\to\infty}\left|\frac{n}{3n+3}\right|???
Since we’ll get the indeterminate form ???\infty/\infty??? if we try to evaluate the limit, we’ll divide the numerator and denominator by the highest-degree variable in order to reduce the fraction.
???L=|x-3|\lim_{n\to\infty}\left|\frac{n}{3n+3}\left(\frac{\frac{1}{n}}{\frac{1}{n}}\right)\right|???
???L=|x-3|\lim_{n\to\infty}\left|\frac{\frac{n}{n}}{\frac{3n}{n}+\frac{3}{n}}\right|???
???L=|x-3|\lim_{n\to\infty}\left|\frac{1}{3+\frac{3}{n}}\right|???
???L=|x-3|\left|\frac{1}{3+\frac{3}{\infty}}\right|???
???L=|x-3|\left|\frac{1}{3+0}\right|???
???L=|x-3|\left|\frac13\right|???
???L=\frac13|x-3|???
To find the interval of convergence, we’ll take the inequality we used to find the radius of convergence, and solve it for x.
Since the ratio test tells us that the series will converge when ???L<1???, so we’ll set up the inequality.
???\frac13|x-3|<1???
???|x-3|<3???
Since the inequality is in the form ???|x-a|<R???, we can say that the radius of convergence is ???R=3???.
To find the interval of convergence, we’ll take the inequality we used to find the radius of convergence, and solve it for ???x???.
???|x-3|<3???
???-3<x-3<3???
???-3+3<x-3+3<3+3???
???0<x<6???
We need to test the endpoints of the inequality by plugging them into the power series representation. We’ll start with ???x=0???.
???\sum^{\infty}_{n=1}\frac{(-1)^{n+1}(0-3)^n}{n3^n}???
???\sum^{\infty}_{n=1}\frac{(-1)^{n+1}(-3)^n}{n3^n}???
???\sum^{\infty}_{n=1}\frac{(-1)^{n+1}(-1)^n(3)^n}{n3^n}???
???\sum^{\infty}_{n=1}\frac{(-1)^{2n+1}}{n}???
The exponent on the ???-1??? will always be odd, so the sum is going to simplify to
???\sum^{\infty}_{n=1}-\frac{1}{n}???
This is a divergent ???p???-series, so the series diverges at the endpoint ???x=0???. Now we’ll test ???x=6???.
???\sum^{\infty}_{n=1}\frac{(-1)^{n+1}(6-3)^n}{n3^n}???
???\sum^{\infty}_{n=1}\frac{(-1)^{n+1}3^n}{n3^n}???
???\sum^{\infty}_{n=1}\frac{(-1)^{n+1}}{n}???
This is an alternating series where
???a_n=\frac{1}{n}???
The alternating series test for convergence says that a series converges if ???\lim_{n\to\infty}a_n=0???.
???\lim_{n\to\infty}\frac{1}{n}???
???\frac{1}{\infty}???
???0???
The series converges at the endpoint ???x=6???.
We’ve shown that the series diverges at ???x=0??? and converges at ???x=6???, which means the interval of convergence is
???0<x\le6???
We’ll summarize our findings.