Plotting points in three dimensions
How to plot points in three dimensions
To plot points in three-dimensional coordinate space, we’ll start with a three dimensional coordinate system, where the ???x???-axis comes toward us on the left, the ???y???-axis moves out toward the right, and the ???z???-axis is perfectly vertical.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
If we need to consider negative values of ???x???, ???y???, or ???z???, then we should know that the negative direction of the ???x???-axis follows the straight line of the positive ???x???-axis away from us, that the negative direction of the ???y???-axis moves out to the left, and that the negative direction of the ???z???-axis is perfectly vertical, extending out below the positive direction of the ???z???-axis.
In the same way that we plot points in two-dimensional coordinate space by moving out along the ???x???-axis to our ???x??? value, and then moving parallel to the ???y???-axis until we find our point, in three-dimensional space we’ll move along the ???x???-axis, then parallel to the ???y???-axis, then parallel to the ???z???-axis until we arrive at our coordinate point.
Video walkthrough of plotting four different points in three-dimensional space
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Another example of how to plot a point in three dimensions
Example
Plot the point in a three-dimensional coordinate system.
???(4,2,3)???
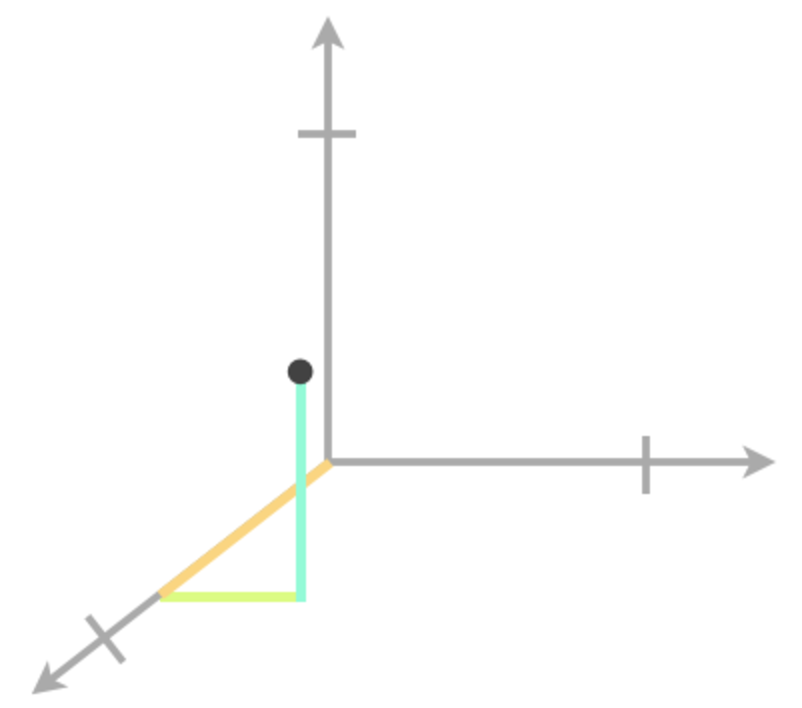
We’ll start by drawing our axes, then moving out from the origin along the ???x???-axis until we get to ???x=4???.
To get to ???(4,2)??? in the ???xy???-plane, we’ll start where we left off on the ???x???-axis, and move parallel to the ???y???-axis until we get to ???y=2???.
To get to ???(4,2,3)??? in three-dimensional space, we’ll start where we left off in the ???xy???-coordinate plane, and move parallel to the ???z???-axis until we get to ???z=3???.
in three-dimensional space we’ll move along the x-axis, then parallel to the y-axis, then parallel to the z-axis until we arrive at our coordinate point.
If we only plot the point, and nothing else, it can be difficult or impossible to identify the location of a three-dimensional point on a two-dimensional piece of paper. To fix this problem, we can fill in the three-dimensional box, putting one corner of the box at the origin, and the opposite corner at the coordinate point we just plotted.
Even though it’s only technically necessary to plot and label the coordinate point, you can see how drawing in the lines we used to get to the point, and the box that connects the origin to the coordinate point, is really helpful in giving us some perspective.