Definite integrals
What does a definite integral actually calculate?
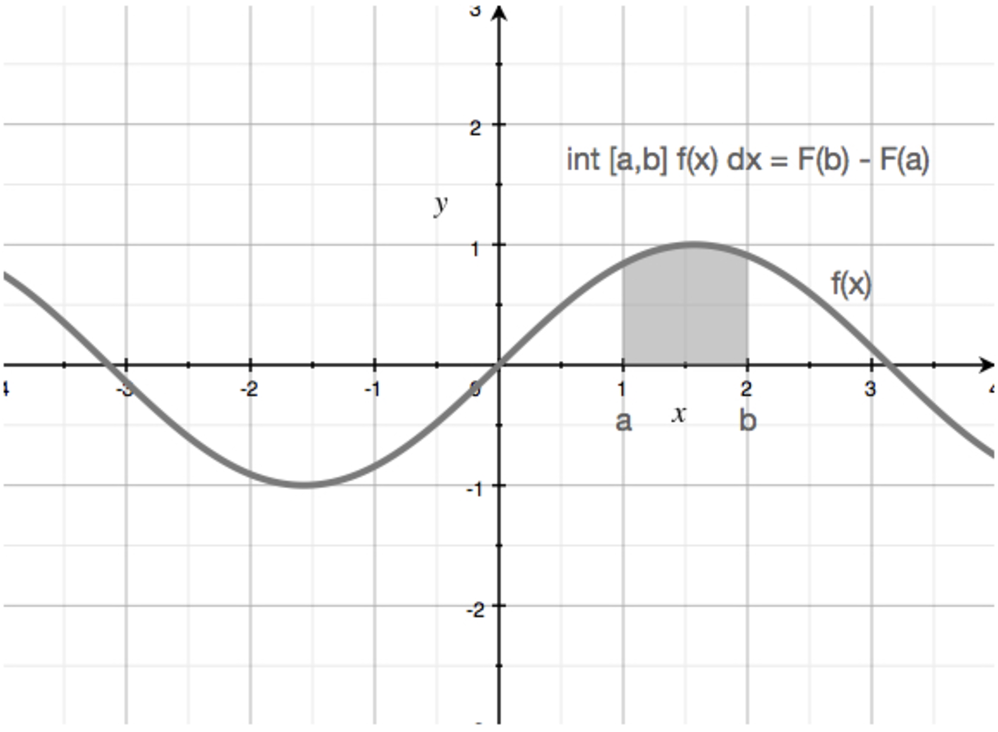
Evaluating a definite integral means finding the area enclosed by the graph of the function and the ???x???-axis, over the given interval ???[a,b]???.
In the graph below, the shaded area is the integral of ???f(x)??? on the interval ???[a,b]???. Finding this area means taking the integral of ???f(x)???, plugging the upper limit ???b??? into the result, and then subtracting from that whatever you get when you plug in the lower limit ???a???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Finding the area under the curve over an interval
Example
Evaluate the integral.
???\int_0^2 3x^2-5x+2\ dx???
If we let ???f(x)=3x^2-5x+2??? and then integrate the polynomial, we get
???F(x)=\left(x^3-\frac{5}{2}x^2+2x+C\right)\bigg|_0^2???
where ???C??? is the constant of integration.
Evaluating on the interval ???[0,2]???, we get
???F(x)=\left[(2)^3-\frac{5}{2}(2)^2+2(2)+C\right]-\left[(0)^3-\frac{5}{2}(0)^2+2(0)+C\right]???
???F(x)=(8-10+4+C)-(0-0+0+C)???
???F(x)=8-10+4+C-C???
???F(x)=2???
As you can see, the constant of integration “cancels out” in the end, leaving a definite value as the final answer, not just a function for ???y??? defined in terms of ???x???.
Since this will always be the case, you can just leave ???C??? out of your answer whenever you’re solving a definite integral.
So, what do we mean when we say ???F(x)=2???? What does this value represent? When we say that ???F(x)=2???, it means that the area
below the graph of ???f(x)???,
above the ???x???-axis, and
between the lines ???x=0??? and ???x=2???
is ???2??? square units.
Video example showing how to calculate a definite integral
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Treating the area below the x-axis as "negative" area
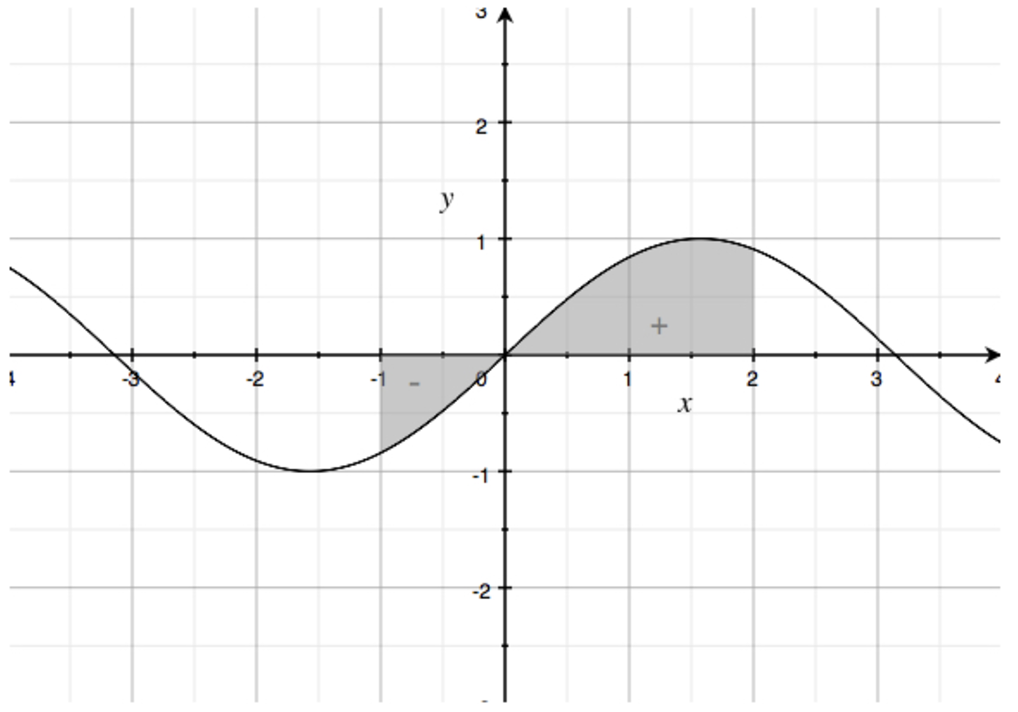
Keep in mind that we’re talking about the area enclosed by the graph and the ???x???-axis. If ???f(x)??? drops below the ???x???-axis inside ???[a,b]???, we treat the area under the ???x???-axis as negative area.
Then finding the value of ???F(x)??? means subtracting the area enclosed by the graph under the ???x???-axis from the area enclosed by the graph above the ???x???-axis.
In other words, evaluating the definite integral of ???f(x)=\sin{x}??? on ???[-1,2]??? means subtracting the area enclosed by the graph below the ???x???-axis from the area enclosed by the graph above the ???x???-axis.
Evaluating a definite integral means finding the area enclosed by the graph of the function and the x-axis
This means that, if the area enclosed by the graph below the ???x???-axis is larger than the area enclosed by the graph above the ???x???-axis, then the value of ???F(x)??? will be negative (???F(x)<0???).
If the area enclosed by the graph below the ???x???-axis is exactly equal to the area enclosed by the graph above the ???x???-axis, then ???F(x)=0???.