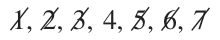How to find mean, median, and mode
Measures of central tendency are different ways of defining “the middle”
We’ve talked a lot about data sets and the individual data points contained within them. And we’ve looked at ways to create visual representations of data.
Now we want to start analyzing the data set in a different way. In this section we’re going to look at what we call measures of central tendency, which are different ways we’ve come up with to describe the “middle,” “center,” or most typical value of the data.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Mean
We usually say “average,” but technically we’re thinking about mean, also called the arithmetic mean. We calculate the mean using a specific formula:
???\mu=\frac{\sum_{i=1}^n x_i}{n}???
In the formula, ???\mu??? (pronounced “mew”) is the mean, ???n??? is the number of items in the data set, and the sum in the numerator tells us to start with the first data point, adding up all the data points together until we get to the last one. In other words, it would be just as correct to write the formula for mean as
???\mu=\frac{\text{the sum of all the data points}}{\text{the number of data points}}???
You can also think about the mean as the “balancing point” of the data. Let’s say that we have the data set ???20,\ 22,\ 26,\ 28???, where the data is evenly spread out. In this case, we can see what the mean is just by looking at the data set. You might predict that the mean is ???24???, and here’s why. We’ll illustrate the data on a number line.
We plotted ???20??? and ???28??? as gray dots, and ???22??? and ???26??? as orange dots. We don’t really need the color coding, because the point we’re trying to illustrate is that we have an equal amount of distance from the mean on the left side as we do on the right side. To be more specific, ???22??? and ???26??? are both ???2??? units away from the mean and ???20??? and ???28??? are both ???4??? units away from the mean.
What this tells us is that whenever we find the mean, what we’re really doing is creating a balance of distance between the points to the left and right of the mean. And in that way, the mean represents the balancing point of all the data. In other words, it’s the point that would balance all of the distances between the points in the data set. If the mean were moved a bit left or right then the balance would tip one way or the other.
Realize also that the formula for calculating the mean doesn’t allow you to find the mean only. If you have the mean, but you’re missing one data point in your set, you could figure out the missing data point.
How to calculate mean, median, and mode for a data set
Take the course
Want to learn more about Probability & Statistics? I have a step-by-step course for that. :)
Finding the missing value in a data set when you already have the mean
Example
Given the data set ???20,\ 22,\ x,\ 28???, and knowing that the mean is ???24???, find the missing value from the data set.
Let’s plug everything we know, including the missing data point, into the formula for the mean.
???\mu=\frac{\text{the sum of all the data points}}{\text{the number of data points}}???
???24=\frac{20+22+x+28}{4}???
Then we just use algebra to solve for the missing data point.
???96=20+22+x+28???
???96-20-22-28=x???
???26=x???
The missing data point is ???26???.
You can also think about the mean as the “balancing point” of the data.
Median
The median of a data set is the value we get when we line up all the data points in the set from least to greatest, and then we look at the number or pair of numbers in the middle.
If we have an odd number of data points, the median will come from one number. For example, take the data set with ???7??? data points:
???1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7???
We need to cross out an equal number of data points on each end of the data set until we get to the number in the center. In this case, we can cross out three data points on each side.
The median is ???4???.
When there are an even number of data points in the set, the process for finding the median is slightly different. In that case, we cross out everything but the middle two terms.
???1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8???
Then to find the median of the data set, we find the mean of the two data points in the middle.
???\mu=\text{median}=\frac{4+5}{2}=\frac92=4.5???
The median is ???4.5???.
Mode
The mode of a data set is the value that occurs most often, more than any other value. You could think about it as the most typical value in the set. In the set ???1,\ 2,\ 3,\ 4,\ 4,\ 6,\ 7???, the mode is ???4??? because ???4??? occurs twice and every other value only occurs once, which means that ???4??? occurs more often than any other value.
Sometimes you’ll have a set like ???1,\ 2,\ 3,\ 4,\ 4,\ 6,\ 6???. In this set, ???4??? and ???6??? occur twice, and every other value occurs once. Which means ???4??? and ???6??? occur most often. Because there’s not a “clear winner” between ???4??? and ???6???, sometimes people will say the data set has no mode, others will say that the set has two modes and the data set is called bi-modal.