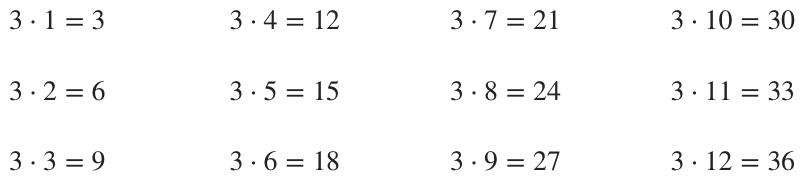Finding the least common multiple (LCM) of a set of numbers
The definition of the least common multiple
A common multiple of two positive whole numbers is a number that’s divisible by both of them. Their least common multiple (sometimes abbreviated LCM) is the smallest number that’s divisible by both of them. For example,
???4??? is the least common multiple of ???2??? and ???4???
???6??? is the least common multiple of ???2??? and ???3???
???10??? is the least common multiple of ???2??? and ???5???
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
When we’re dealing with small numbers, the easiest way to find the least common multiple is to start with the larger number, and test each of its positive multiples, one at a time starting with the smallest one, until we find one that’s divisible by the other number.
Remember, the positive multiples of a positive whole number are the values we get when we multiply it by ???1???, ???2???, ???3???, ???4???, etc. For example, here’s how we get the first twelve positive multiples of ???3???:
Finding the least common multiple of a set of numbers
Take the course
Want to learn more about Pre-Algebra? I have a step-by-step course for that. :)
An example with small numbers
Example
Find the least common multiple of ???3??? and ???4???.
Since ???4??? is the larger number, we’ll use its positive multiples (???4\cdot 1???, ???4\cdot 2???, etc.) to find the smallest one that ???3??? divides into evenly.
Sometimes we need to find the least common multiple of larger numbers, where using this method might be more difficult. In this case, we can use a different method for finding the least common multiple: finding the prime factorization of each number, and then using the prime factors to build the least common multiple.
A common multiple of two positive whole numbers is a number that’s divisible by both of them. Their least common multiple is the smallest number that’s divisible by both of them.
Example
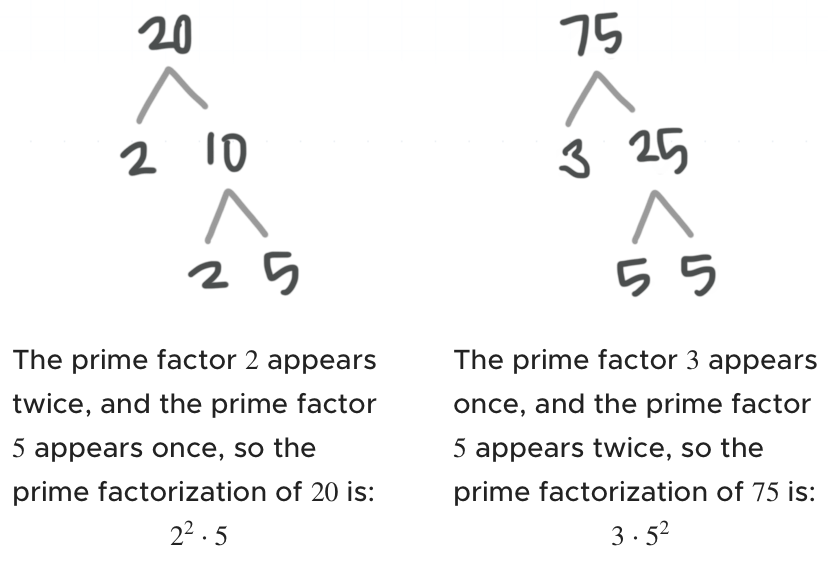
Find the least common multiple of ???20??? and ???75???.
We need to reduce each of these numbers to its prime factors.
We found prime factors of ???2???, ???3???, and ???5???. The number of times each of these prime factors appears in the least common multiple of ???20??? and ???75??? will be the larger of the number of times it appears in the prime factorization of ???20??? and the number of times it appears in the prime factorization of ???75???.
There are two factors of ???2??? in ???20???, and none in ???75???, so there will be two factors of ???2??? in their least common multiple.
There are no factors of ???3??? in ???20???, and one in ???75???, so there will be one factor of ???3??? in their least common multiple.
There is one factor of ???5??? in ???20???, and there are two in ???75???, so there will be two factors of ???5??? in their least common multiple.
Therefore, the least common multiple of ???20??? and ???75??? is ???2^2\cdot3\cdot5^2???. Now we’ll multiply this out to express the least common multiple as a single number:
???2^2\cdot 3\cdot 5^2???
???4\cdot 3\cdot 25???
???12\cdot 25???
???300???
This tells us that ???300??? is the least common multiple of ???20??? and ???75???.
Remember, we can always double-check our answer by dividing the least common multiple by the original numbers. Using the previous example, we said that ???300??? was the least common multiple of ???20??? and ???75???. If that’s true, then ???20??? and ???75??? must both go evenly into ???300???.
???300\div20=15???
???300\div 75=4???
Because we got whole numbers for answers, we know that ???300??? is a common multiple of ???20??? and ???75???. In fact, ???300??? is the least common multiple of ???20??? and ???75???: When we divide ???300??? by ???20??? and ???75???, we get ???15??? and ???4???, respectively, and the only number by which both ???15??? and ???4??? are divisible is ???1???.