Finding the area inside both polar curves
Defining the area inside two polar curves
The area inside both curves is the area which is enclosed by both curves.
For example, given the polar curves 1. ???r=2??? and 2. ???r=4???, only the area inside ???r=2??? is inside both curves.
Some of the area inside ???r=4??? is outside of ???r=2???, so that area isn’t inside both curves.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
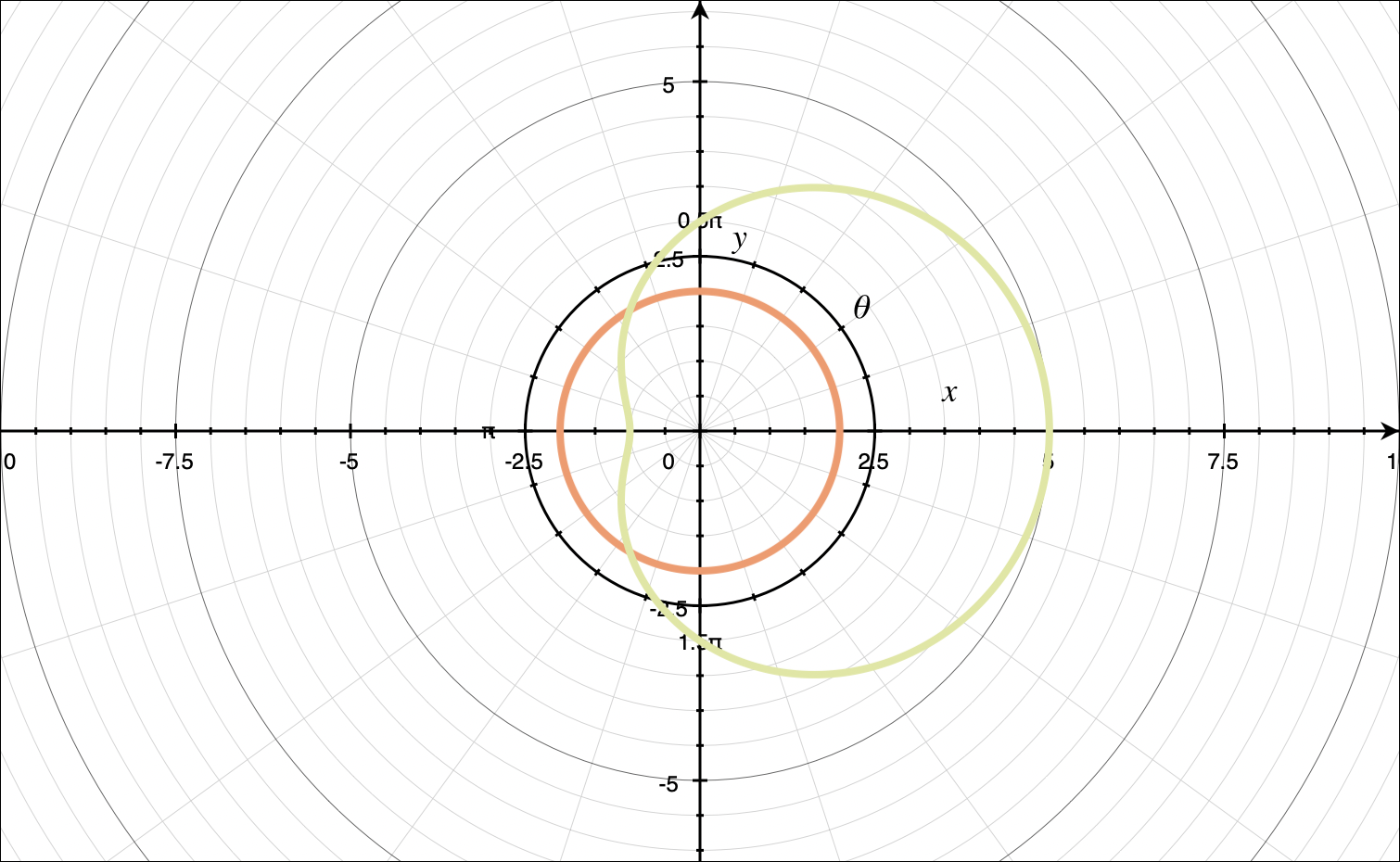
Unfortunately, not all of these kinds of problems will be this easy. There will always be multiple ways to go about finding the area inside both polar curves. For example, given the curves 1. ???r=3\sin{\theta}??? and 2. ???r=3\cos{\theta}??? whose graphs are
we could
find the area inside ???r=3\sin{\theta}??? and then subtract the area inside ???r=3\sin{\theta}??? but outside ???r=3\cos{\theta}???
find the area inside ???r=3\cos{\theta}??? and then subtract the area inside ???r=3\cos{\theta}??? but outside ???r=3\cos{\theta}???
Some sections of area will be easier to solve for than others. Therefore, the best way to solve for the area inside both curves is to graph them, then based on the graphs, look for the easiest areas to calculate and use those to go about finding the area inside both curves.
How to determine which curve is the inner curve and which is the outer, then calculate the area contained inside both curves at the same time
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Finding the area of the region enclosed by both polar curves
Example
Find the area of the region enclosed by both polar curves.
???r=2???
???r=3+2\cos{\theta}???
We’ll graph the given curves to see what we’re dealing with.
From the graph, we can see that most of 1. ???r=2??? is also enclosed by 2. ???r=3+2\cos{\theta}???. To find the area inside both curves, we could
use ???A_T=A_1-A_2???, where
???A_T??? is the area inside both curves
???A_1??? is all of the area inside ???r=3+2\cos{\theta}???
???A_2??? is the area inside ???r=3+2\cos{\theta}??? but outside ???r=2???
use ???A_T=A_1-A_2???, where
???A_T??? is the area inside both curves
???A_1??? is all of the area inside ???r=2???
???A_2??? is the area inside ???r=2??? but outside ???r=3+2\cos{\theta}???
Since finding the area inside ???r=2??? is a little easier than finding the area inside ???r=3+2\cos{\theta}???, we’ll use the second option.
To find the area inside ???r=2???, we’ll use the area formula over the interval ???[0,2\pi]???.
???A_1=\int^{\beta}_{\alpha}\frac12r^2\ d\theta???
???A_1=\int^{2\pi}_0\frac12(2)^2\ d\theta???
???A_1=\int^{2\pi}_02\ d\theta???
???A_1=2\theta\big|^{2\pi}_0???
???A_1=2(2\pi)-2(0)???
???A_1=4\pi???
To find the area inside ???r=2??? but outside ???r=3+2\cos{\theta}???, we’ll find the intersection points and then use the formula
???A_2=\int^{\beta}_{\alpha}\frac{1}{2}\left(r^2_O-r^2_I\right)\ d\theta???, where
???r_O=2???
???r_I=3+2\cos{\theta}???
We’ll find the intersection points by setting the polar equations equal to each other and solving for ???\theta???.
???2=3+2\cos{\theta}???
???-\frac12=\cos{\theta}???
???\theta=\frac{2\pi}{3},\ \frac{4\pi}{3}???
The interval for this section of area is
???[\alpha,\beta]=\left[\frac{2\pi}{3},\frac{4\pi}{3}\right]???
If instead we wanted to find the area of outside ???r=2??? but inside ???r=3+2\cos{\theta}???, we’d have to change the interval to ???[\alpha,\beta]=\left[-\frac{2\pi}{3},\frac{2\pi}{3}\right]???.
Plugging everything we know about that ???A_2??? into the area formula, we get
???A_2=\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}\frac12\left[(2)^2-(3+2\cos{\theta})^2\right]\ d\theta???
???A_2=\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}4-\left(9+12\cos{\theta}+4\cos^2{\theta}\right)\ d\theta???
???A_2=\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}4-9-12\cos{\theta}-4\cos^2{\theta}\ d\theta???
???A_2=\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}-5-12\cos{\theta}-4\cos^2{\theta}\ d\theta???
???A_2=-\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}4\cos^2{\theta}+12\cos{\theta}+5\ d\theta???
the best way to solve for the area inside both curves is to graph them, then based on the graphs, look for the easiest areas to calculate and use those to go about finding the area inside both curves.
Since ???\cos^2{\theta}=\frac12\left[1+\cos{(2\theta)}\right]???,
???A_2=-\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}4\left[\frac12\left[1+\cos{(2\theta)}\right]\right]+12\cos{\theta}+5\ d\theta???
???A_2=-\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}2\left[1+\cos{(2\theta)}\right]+12\cos{\theta}+5\ d\theta???
???A_2=-\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}2+2\cos{(2\theta)}+12\cos{\theta}+5\ d\theta???
???A_2=-\frac12\int^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}2\cos{(2\theta)}+12\cos{\theta}+7\ d\theta???
???A_2=-\frac12\left[\sin{(2\theta)}+12\sin{\theta}+7\theta\right]\Big|^{\frac{4\pi}{3}}_{\frac{2\pi}{3}}???
Evaluate over the interval.
???A_2=-\frac12\left[\sin{\left(2\cdot\frac{4\pi}{3}\right)}+12\sin{\frac{4\pi}{3}}+7\cdot\frac{4\pi}{3}\right]+\frac12\left[\sin{\left(2\cdot\frac{2\pi}{3}\right)}+12\sin{\frac{2\pi}{3}}+7\cdot\frac{2\pi}{3}\right]???
???A_2=-\frac12\left(\sin{\frac{8\pi}{3}}+12\sin{\frac{4\pi}{3}}+\frac{28\pi}{3}\right)+\frac12\left(\sin{\frac{4\pi}{3}}+12\sin{\frac{2\pi}{3}}+\frac{14\pi}{3}\right)???
Simplify the trigonometric functions.
???A_2=-\frac12\left[\frac{\sqrt{3}}{2}+12\left(-\frac{\sqrt{3}}{2}\right)+\frac{28\pi}{3}\right]+\frac12\left[\left(-\frac{\sqrt{3}}{2}\right)+12\left(\frac{\sqrt{3}}{2}\right)+\frac{14\pi}{3}\right]???
???A_2=-\frac12\left(\frac{\sqrt{3}}{2}-\frac{12\sqrt{3}}{2}+\frac{28\pi}{3}\right)+\frac12\left(-\frac{\sqrt{3}}{2}+\frac{12\sqrt{3}}{2}+\frac{14\pi}{3}\right)???
???A_2=-\frac12\left(-\frac{11\sqrt{3}}{2}+\frac{28\pi}{3}\right)+\frac12\left(\frac{11\sqrt{3}}{2}+\frac{14\pi}{3}\right)???
???A_2=\frac{11\sqrt{3}}{4}-\frac{28\pi}{6}+\frac{11\sqrt{3}}{4}+\frac{14\pi}{6}???
???A_2=\frac{22\sqrt{3}}{4}-\frac{14\pi}{6}???
???A_2=\frac{11\sqrt{3}}{2}-\frac{7\pi}{3}???
Find a common denominator.
???A_2=\frac{33\sqrt{3}}{6}-\frac{14\pi}{6}???
???A_2=\frac{33\sqrt{3}-14\pi}{6}???
Our last step is to solve for ???A_T??? using ???A_T=A_1-A_2???.
???A_T=4\pi-\frac{33\sqrt{3}-14\pi}{6}???
???A_T=\frac{24\pi-33\sqrt{3}+14\pi}{6}???
???A_T=\frac{38\pi-33\sqrt{3}}{6}???