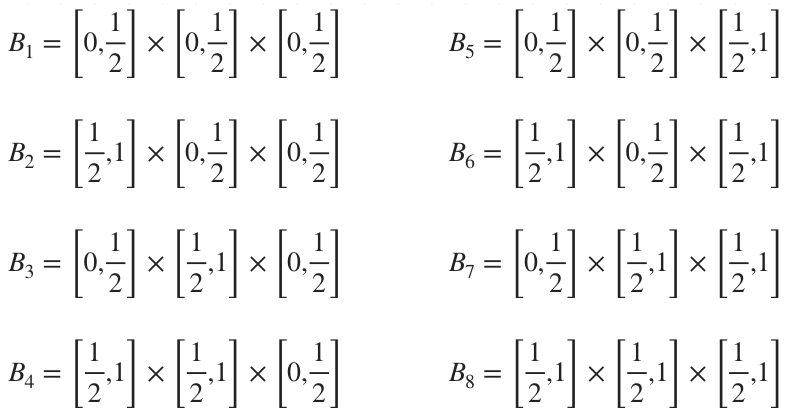Solving triple integrals using the midpoint rule
Midpoint rule for triple integrals vs. midpoint rule for double integrals
We can approximate the value of a triple integral using midpoint rule for triple integrals.
Similarly to the way we used midpoints to approximate single integrals by taking the midpoint at the top of each approximating rectangle, and to the way we used midpoints to approximate double integrals by taking the midpoint at the top of each approximating prism, we can use midpoints to approximate a triple integral by taking the midpoint of each sub-cube.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The midpoint rule for triple integrals is
???\int\int\int_Bf(x,y,z)\ dV\approx\sum^m_{i=1}\sum^n_{j=1}\sum^o_{k=1}f(\overline{x_i},\overline{y_j},\overline{z_k})\ \Delta{V}???
where ???B??? is the region for which we want to find volume, ???m??? is the number of subintervals in the ???x??? direction, ???n??? is the number of subintervals in the ???y??? direction, ???o??? is the number of subintervals in the ???z??? direction, and ???\Delta V??? is the volume of one of the sub-cubes.
Once we define the boundaries of each sub-cube, we can take the midpoints of each of them, and then plug them into the midpoint formula, along with ???\Delta V???.
Solving triple integrals by breaking down the region into sub-cubes and then using their midpoints
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Using the midpoint rule with 8 equal sub-cubes to evaluate a triple integral
Example
Use midpoint rule with ???8??? equal sub-cubes to estimate the volume of the triple integral.
???\int\int\int_B\sin{(2xyz)}\ dV???
where ???B=\left\{(x,y,z)|0\le{x}\le1,0\le{y}\le1,0\le{z}\le1\right\}???
???B??? is the cube with one corner at the origin, and side length ???1???, such that ???B=[0,1]\times[0,1]\times[0,1]???. Since we need to use ???8??? sub-cubes, that means we’ll have to divide each side of the cube in half to find the edges of the sub-boxes.
For example, the sub-cube whose corner is on the origin is defined by
???B_1=\left[0,\frac12\right]\times\left[0,\frac12\right]\times\left[0,\frac12\right]???
If we head in the positive direction of the ???x???-axis and take the second sub-cube, it’s defined by
???B_2=\left[\frac12,1\right]\times\left[0,\frac12\right]\times\left[0,\frac12\right]???
Our ???8??? sub-cubes can be defined as
To find midpoint of each cube, we just take the value halfway between the edges of each interval, such that the midpoints are
Next we need to solve for ???\Delta {V}???. We’ll use the dimensions of one of the smaller cubes to find ???\Delta {V}???.
???V_{B_1}=\Delta V=\left(\frac12\right)\left(\frac12\right)\left(\frac12\right)???
???\Delta {V}=\frac18???
Once we define the boundaries of each sub-cube, we can take the midpoints of each of them, and then plug them into the midpoint formula.
Plugging everything into the midpoint formula, we get
???V\approx\frac18\Bigg\{\sin{\left[2\left(\frac14\right)\left(\frac14\right)\left(\frac14\right)\right]}+\sin{\left[2\left(\frac34\right)\left(\frac14\right)\left(\frac14\right)\right]}???
???+\sin{\left[2\left(\frac14\right)\left(\frac34\right)\left(\frac14\right)\right]}+\sin{\left[2\left(\frac34\right)\left(\frac34\right)\left(\frac14\right)\right]}???
???+\sin{\left[2\left(\frac14\right)\left(\frac14\right)\left(\frac34\right)\right]}+\sin{\left[2\left(\frac34\right)\left(\frac14\right)\left(\frac34\right)\right]}???
???+\sin{\left[2\left(\frac{1}{4}\right)\left(\frac{3}{4}\right)\left(\frac{3}{4}\right)\right]}+\sin{\left[2\left(\frac{3}{4}\right)\left(\frac{3}{4}\right)\left(\frac{3}{4}\right)\right]}\Bigg\}???
???V\approx\frac18\Bigg[\sin{\left(\frac{1}{32}\right)}+\sin{\left(\frac{3}{32}\right)}+\sin{\left(\frac{3}{32}\right)}+\sin{\left(\frac{9}{32}\right)}???
???+\sin{\left(\frac{3}{32}\right)}+\sin{\left(\frac{9}{32}\right)}+\sin{\left(\frac{9}{32}\right)}+\sin{\left(\frac{27}{32}\right)}\Bigg]???
???V\approx\frac18\Bigg[\sin{\left(\frac{1}{32}\right)}+3\sin{\left(\frac{3}{32}\right)}+3\sin{\left(\frac{9}{32}\right)}+\sin{\left(\frac{27}{32}\right)}\Bigg]???
???V\approx\frac18(0.0312+0.2808+0.8327+0.7471)???
???V\approx\frac18(1.8918)???
???V\approx0.2365??? cubic units
This is the volume of the cube ???B???, which we found using midpoint rule for triple integrals.