Midsegments of triangles and the triangle midsegment theorem
Midsegments divide the sides of a triangle exactly in half
In this lesson we’ll define the midsegment of a triangle and use a midsegment to solve for missing lengths.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Midsegment of a triangle
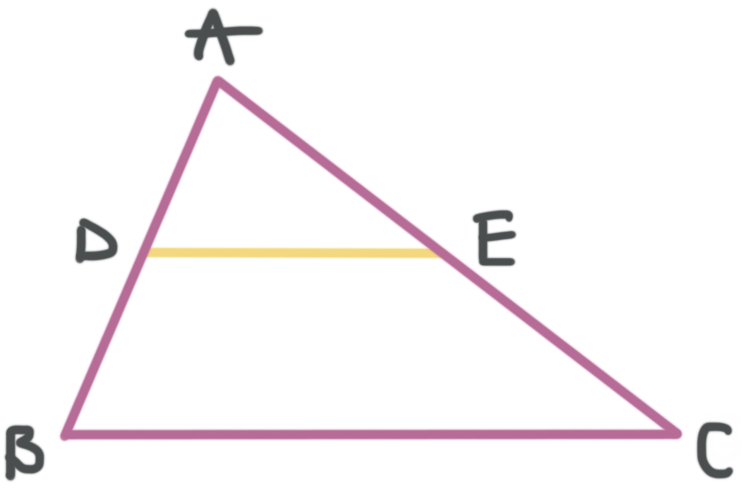
Like the side-splitting segments we talked about in the previous section, a midsegment in a triangle is a line drawn across a triangle from one side to another, parallel to the side it doesn’t touch. The difference between any other side-splitting segment and a midsegment, is that the midsegment specifically divides the sides it touches exactly in half. So in the figure below, ???\overline{DE}??? cuts ???\overline{AB}??? and ???\overline{AC}??? exactly in half.
Remember the midpoint has the special property that it divides the triangle’s sides into two equal parts, which means that ???\overline{AD}=\overline{DB}??? and ???\overline{AE}=\overline{EB}???.
Triangles have three possible midsegments
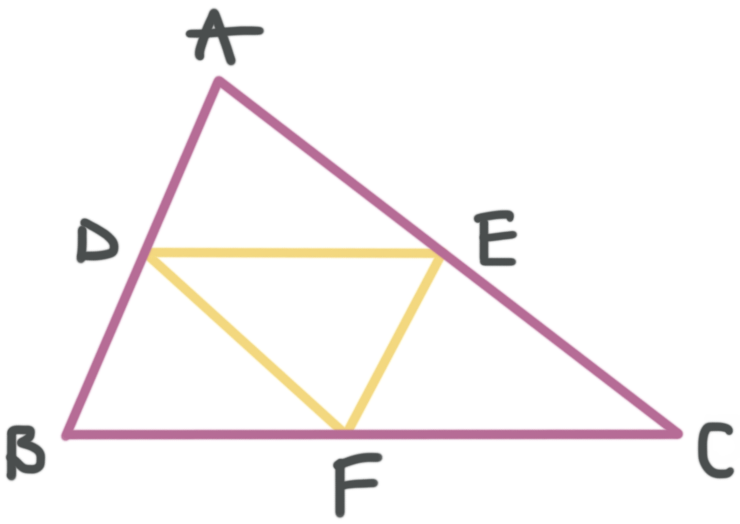
If ???D??? is the midpoint of ???\overline{AB}???, ???E??? is the midpoint of ???\overline{AC}???, and ???F??? is the midpoint of ???\overline{BC}???, then ???\overline{DE}???, ???\overline{DF}???, and ???\overline{EF}??? are all midsegments of triangle ???ABC???.
There are two special properties of a midsegment of a triangle that are part of the midsegment of a triangle theorem.
Midsegment of a triangle theorem
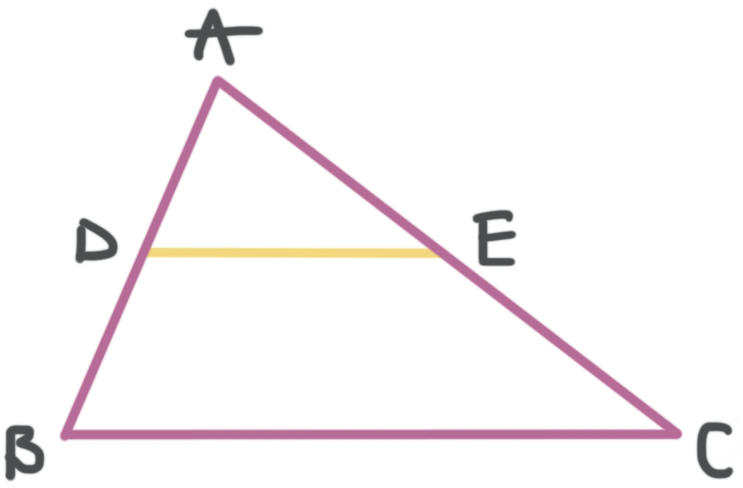
The midsegment of a triangle is parallel to the third side of the triangle and it’s always equal to ???1/2??? of the length of the third side. This means that if you know that ???\overline{DE}??? is a midsegment of this triangle,
then
???\overline{DE}\parallel\overline{BC}??? and ???DE=(1/2)BC???
Then it’s also logical to say that, if you know ???F??? is the midpoint of ???\overline{BC}???, then ???DE=BF=FC???.
Working with midsegments to solve for other values in the triangle
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Solving for x when you’re given the length of the midsegment
Example
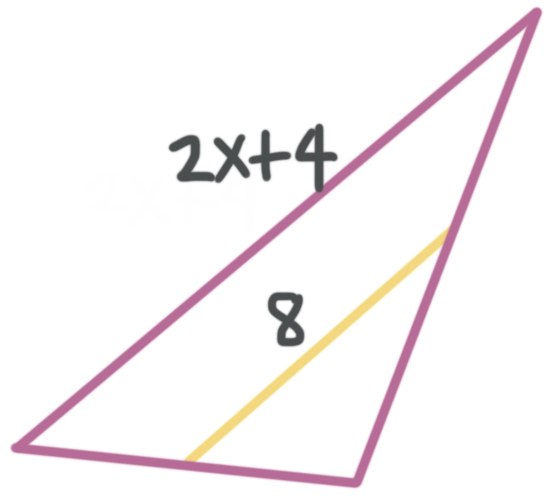
If ???8??? is the midsegment of the triangle, what’s the value of ???x????
Because the midsegment of the triangle has a length of ???8??? we can say
???8=\frac{1}{2}(2x+4)???
???8=x+2???
???6=x???
a midsegment in a triangle is a line drawn across a triangle from one side to another, parallel to the side it doesn’t touch.
How to find the perimeter of a triangle when you have midsegment lengths and the length of one side
Example
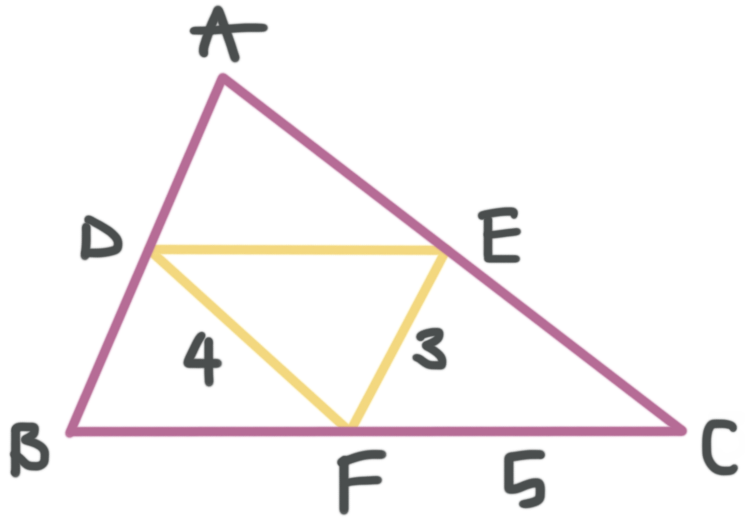
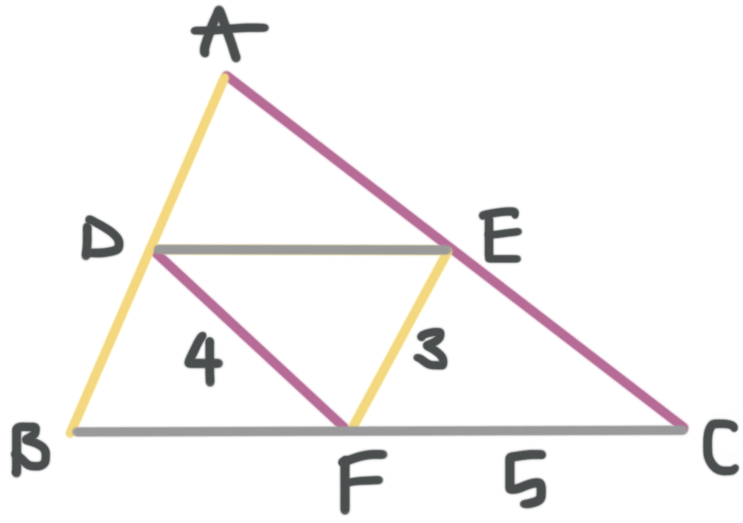
If ???D??? is the midpoint of ???\overline{AB}???, ???E??? is the midpoint of ???\overline{AC}???, and ???F??? is the midpoint of ???\overline{BC}???, find the perimeter of triangle ???ABC???.
???\overline{DE}???, ???\overline{DF}???, and ???\overline{EF}??? are all midsegments of triangle ???ABC???, which means we can use the fact that the midsegment of a triangle is half the length of the third side in order to fill in the triangle.
Let’s color code which midsegment goes with each side.
Now we can fill in what we know.
To find the perimeter, we’ll just add all the outside lengths together.
???P=3+3+4+4+5+5???
???P=24???