How to use the squeeze theorem
How to find the limit at a point where the function is undefined
The squeeze theorem allows us to find the limit of a function at a particular point, even when the function is undefined at that point. The way that we do it is by showing that our function can be squeezed between two other functions at the given point, and proving that the limits of these other functions are equal to one another.
If you think about it, if you can show that two functions have the same value at the same point, and you know that your original function has to run through the other two (be squeezed, or pinched, or sandwiched between them), then the original function can’t take on any possible value other than the value of the other two at that particular point.
Let’s get a little more technical and take a look at the actual theorem.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The Squeeze Theorem
We assume that our original function is ???h(x)???, and that it’s squeezed between two other functions, ???f(x)??? and ???g(x)???, so
???f(x)\leq h(x)\leq g(x)???
We also assume that the limits of our other two functions are equal as we approach the point we’re interested in, so
???\lim_{x \to c} f(x)=\lim_{x \to c} g(x)=L???
If we can show that both of the above statements are true, then we know that our original function has the same limit as the other two function, and we say
???\lim_{x \to c} h(x)=L???
We don’t need to know what’s actually happening to ???h(x)??? at ???x=c???. We’re only concerned with the limit, so we just need to know what’s happening around ???x=c???.
Applying the Squeeze Theorem to find the limit at a specific point
Take the course
Want to learn more about Calculus 1? I have a step-by-step course for that. :)
Applying the Squeeze Theorem to find the value of the limit
Example
Evaluate the limit.
???\lim_{x \to 0} x^2\sin{\left(\frac{1}{x}\right)}???
First we notice that direct substitution will not work since we have ???1/x??? as part of our equation and ???1/0??? does not exist. This shows us that there is a continuity break at ???x=0??? for our function, but we need to find the limits, so we need to break down what we know.
Let’s start with something simple. We know that
???-1\leq \sin{x}\leq 1???
Which means that
???-1\leq \sin{\left(\frac{1}{x}\right)}\leq 1???
We really want to have our original equation in our inequality, which at this point, we can easily do by multiplying each part of the inequality by ???x^2???.
???-x^2\leq x^2\sin{\left(\frac{1}{x}\right)}\leq x^2???
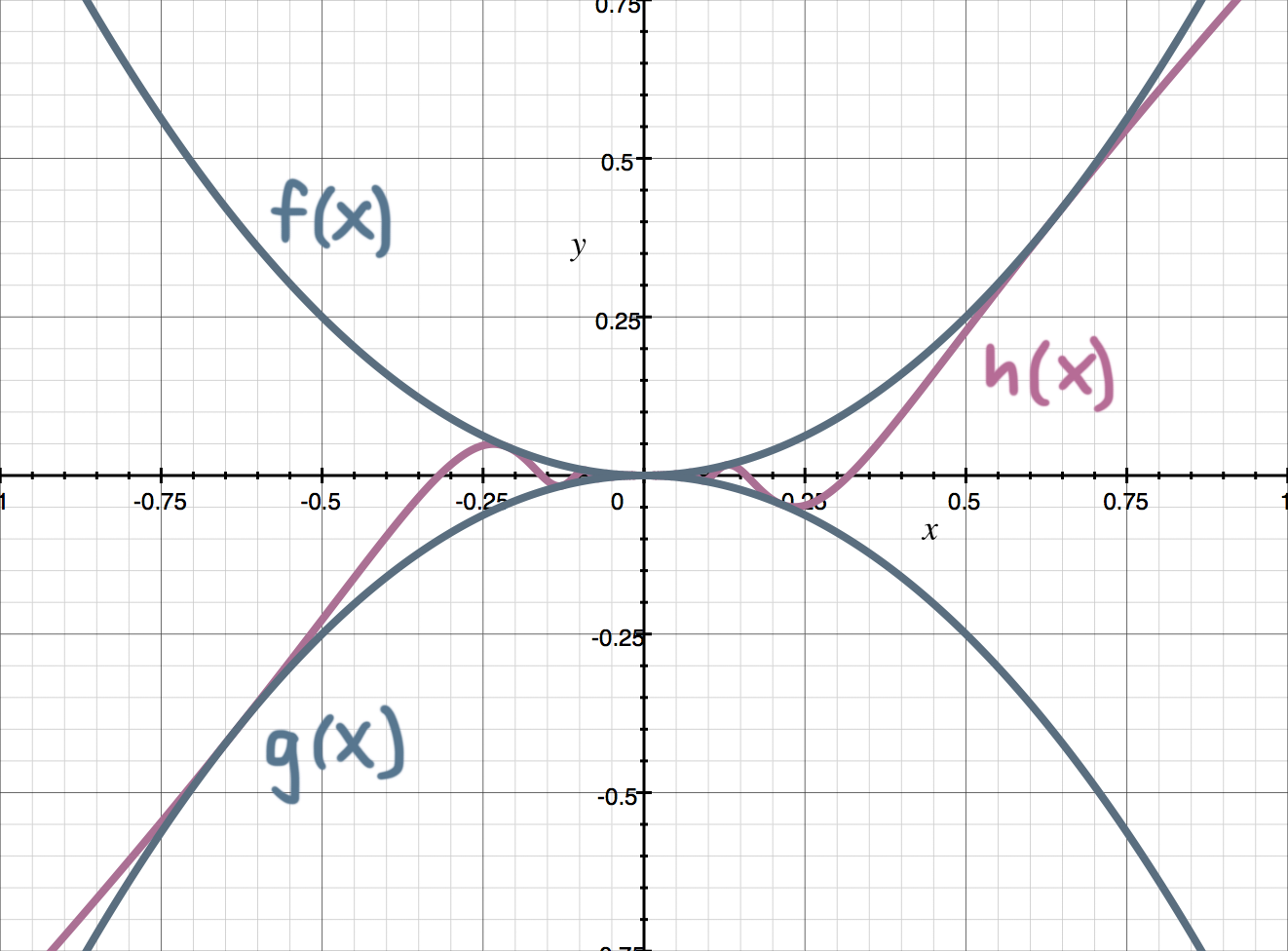
The Squeeze Theorem proves the value of a limit by squeezing it between equal values
We have now “squeezed” our original function between two other functions, and both of those are easy to evaluate as ???x??? approaches ???0???.
???\lim_{x \to 0} x^2=(0)^2=0???
???\lim_{x \to 0}(-x^2)=-(0^2)=0???
Since these two functions have the same limit as ???x??? approaches ???0???, and we know that our original function is squeezed between the other two, there’s no possible value of the limit of our original function at this point other than
???\lim_{x \to 0} x^2\sin{\left(\frac{1}{x}\right)}=0???
The graph below confirms that the three equations all exist as they approach ???x=0??? from both the left-hand and right-hand sides, and that they all have the same value (???y=0???). Remember
???h(x)=x^2\sin{\left(\frac{1}{x}\right)}??? and ???f(x)=x^2??? and ???g(x)=-x^2???