Reflecting figures in coordinate space
Reflections flip a preimage over a line to create the image
In this lesson we’ll look at how the reflection of a figure in a coordinate plane determines where it’s located.
A reflection is a type of transformation that flips a figure over a line. The line is called the line of reflection, or the mirror line. The line of reflection can be horizontal, vertical, or diagonal.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Preimage/image
A transformation of a shape always starts with the preimage. The preimage is usually labeled with capital letters. After the preimage is reflected, the final version of the figure is called the image, which is usually labeled with the same capital letters, plus the prime symbol, ???'???. So if figure ???ABCD??? is reflected, its image becomes figure ???A'B'C'D'???.
The image and preimage are always congruent to each other, because the reflection never changes the angles measures or side lengths of the figure.
Reflecting figures
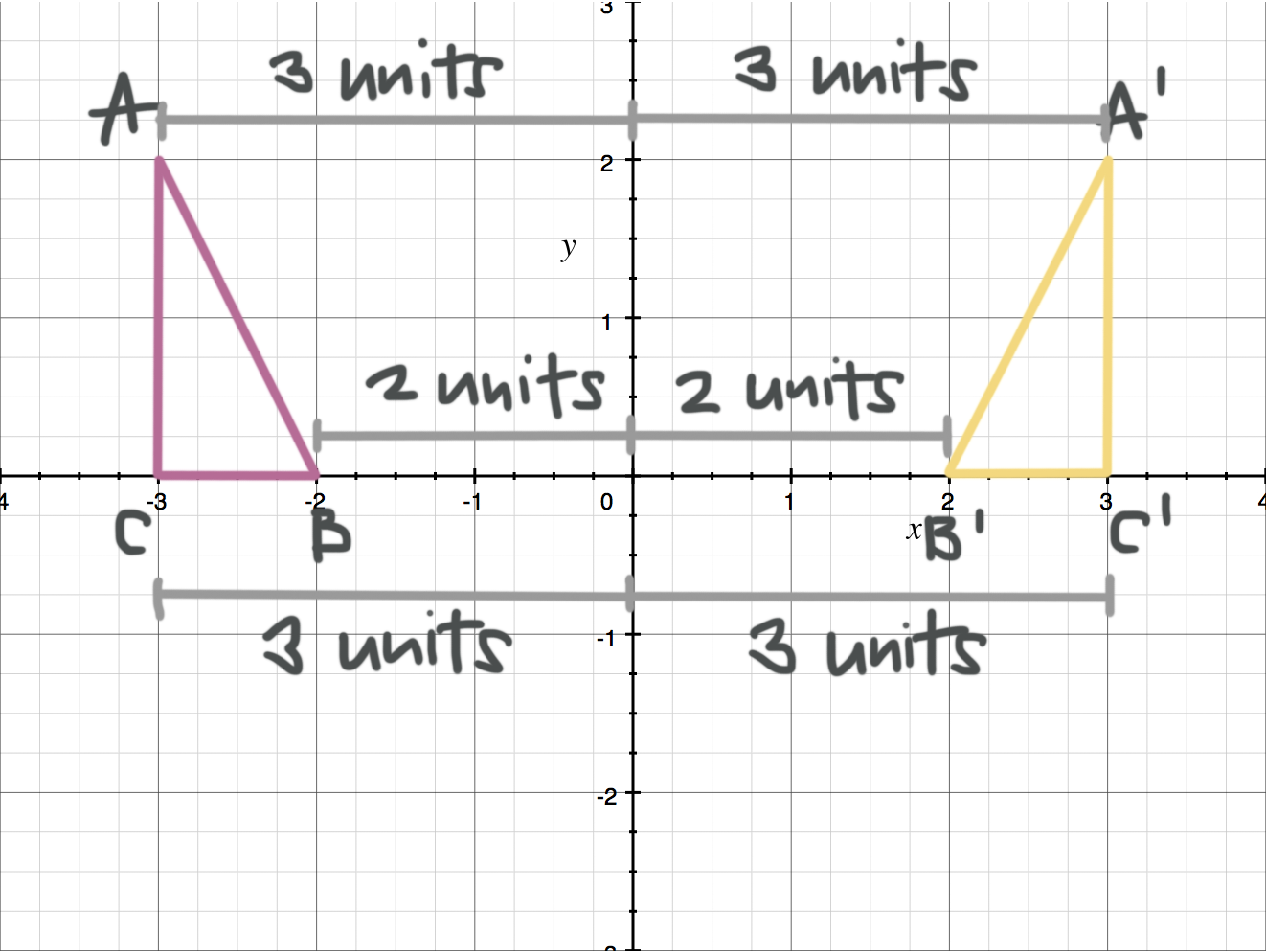
To reflect a figure over a line, the points are the same distance from the line of reflection. Each point from the preimage is the same distance from the ???y???-axis as its matching point in the image.
Notice when we reflect over the ???y???-axis, so the ???x???-values are changing their sign.
???A=(-3,2)??? becomes ???A'=(3,2)???
???B=(-2,0)??? becomes ???B'=(2,0)???
???C=(-3,0)??? becomes ???C'=(3,0)???
Here are some commonly used reflections and their rules.
How to sketch reflections in coordinate space
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Reflecting a triangle across the x-axis
Example
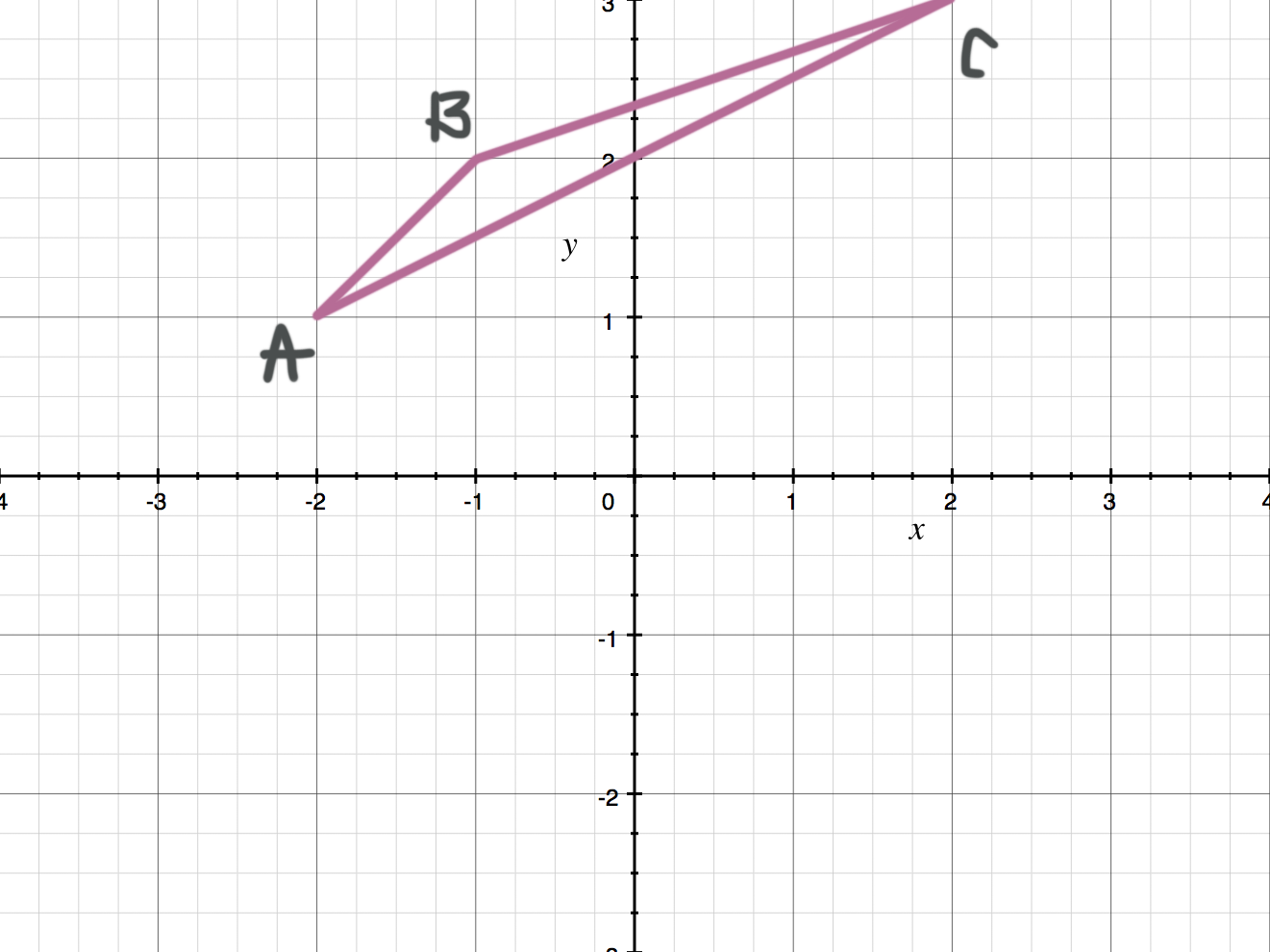
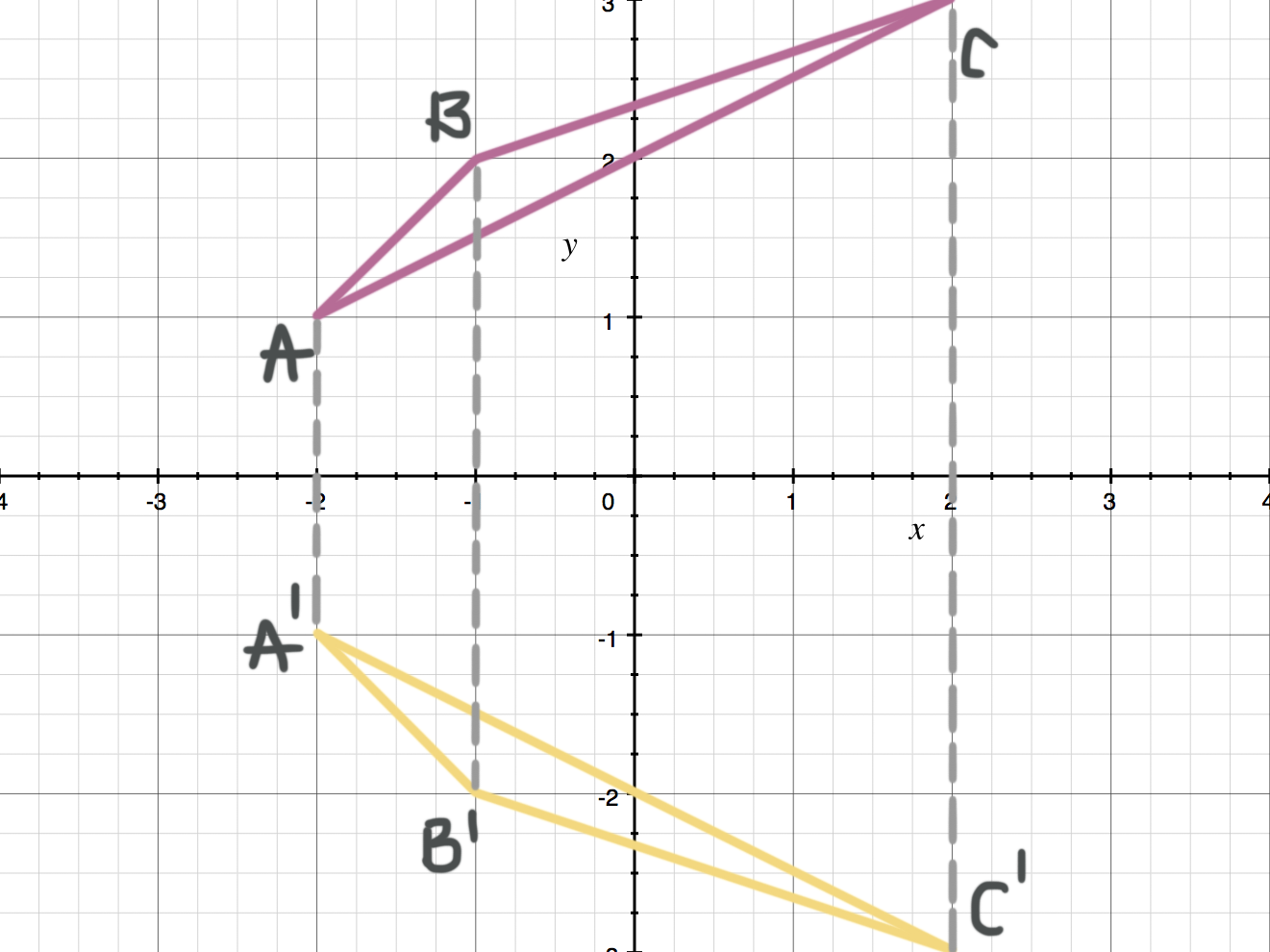
Draw ???\triangle ABC??? after it’s been reflected across the ???x???-axis.
Let’s look at one vertex of the triangle at a time.
Point ???A??? is ???1??? unit above the ???x???-axis, so ???A'??? will be ???1??? unit below the ???x???-axis.
Point ???B??? is ???2??? units above the ???x???-axis, so ???B'??? will be ???2??? units below the ???x???-axis.
Point ???C??? is ???3??? units above the ???x???-axis, so ???C'??? will be ???3??? units below the ???x???-axis.
This means when you reflect across the ???x???-axis, the ???y???-coordinates will change signs.
Let’s look another example.
To reflect a figure over a line, the points are the same distance from the line of reflection.
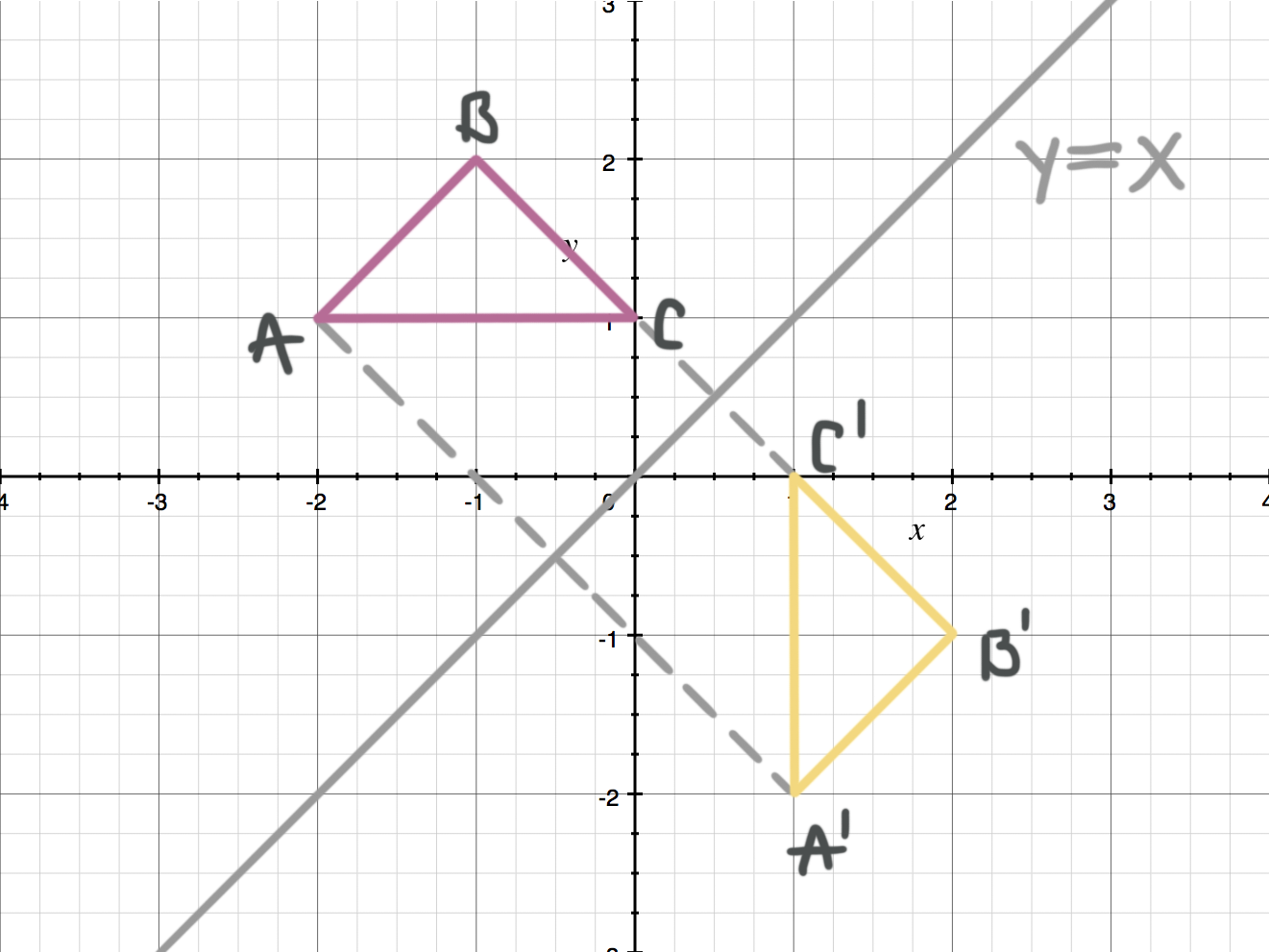
Reflecting a triangle across the line y=x
Example
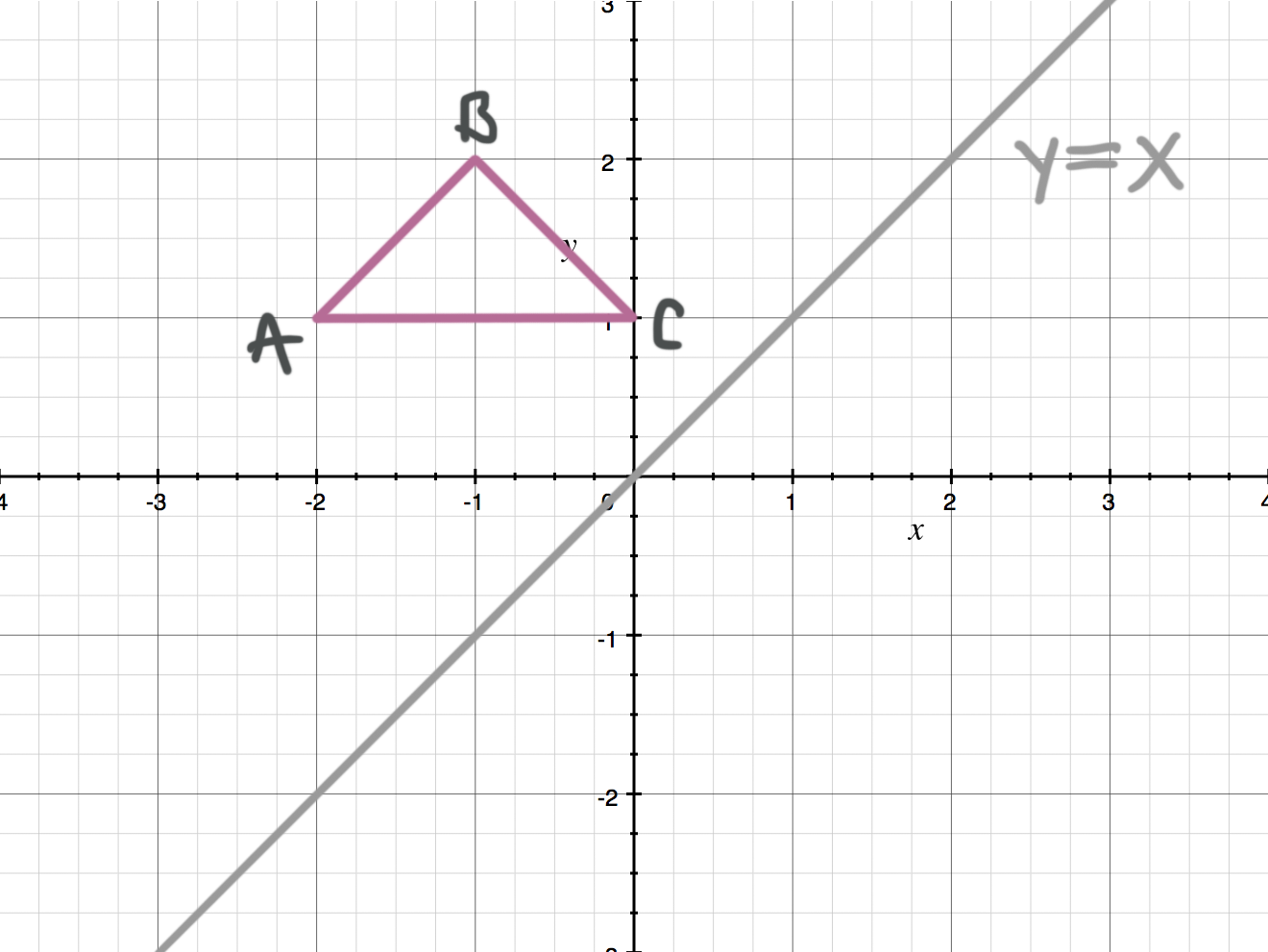
Reflect triangle ???ABC??? across the line ???y=x???.
When you reflect across the line ???y=x???, the ???x???- and ???y???-values switch places. Let’s write down the coordinates of the triangle.
???A=(-2,1)???
???B=(-1,2)???
???C=(0,1)???
Now to reflect the triangle over the line, let’s switch the ???x???- and ???y???-values in each coordinate point.
???A=(-2,1)??? becomes ???A'=(1,2)???
???B=(-1,2)??? becomes ???B'=(2,-1)???
???C=(0,1)??? becomes ???C'=(1,0)???
Then you can plot the image.