Modeling a piecewise-defined function from its graph
Building a piecewise function from its graph
In this lesson we’ll look at piecewise-defined functions and how to write the equation of the definition of such a function given its graph.
A piecewise-defined function (also called a piecewise function) is a function that’s made up of different “pieces,” each of which has its own “sub-function” (its own algebraic expression) and its own “sub-domain” (its own part of the domain of the entire piecewise function).
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
We’ll call the “sub-function” for each piece the function for that piece. A piecewise function is defined by giving the algebraic expression for the function for each piece and its domain. The domain of a piece of a piecewise function can be either an interval or just a single point.
The definition of a piecewise function is written in this form:
???f(x)=\begin{cases}\text{Function}_1 & \quad x\text{-values}\\\text{Function}_2 & \quad x\text{-values} \\\text{Function}_3 & \quad x\text{-values}\\\text{Function}_4 & \quad x\text{-values}\end{cases}???
Of course a piecewise function doesn’t need to have four pieces. It can have anywhere from two pieces to an infinite number of pieces. Usually, there are only two or three.
Let’s look at an example of a definition of a piecewise function and how to graph the function.
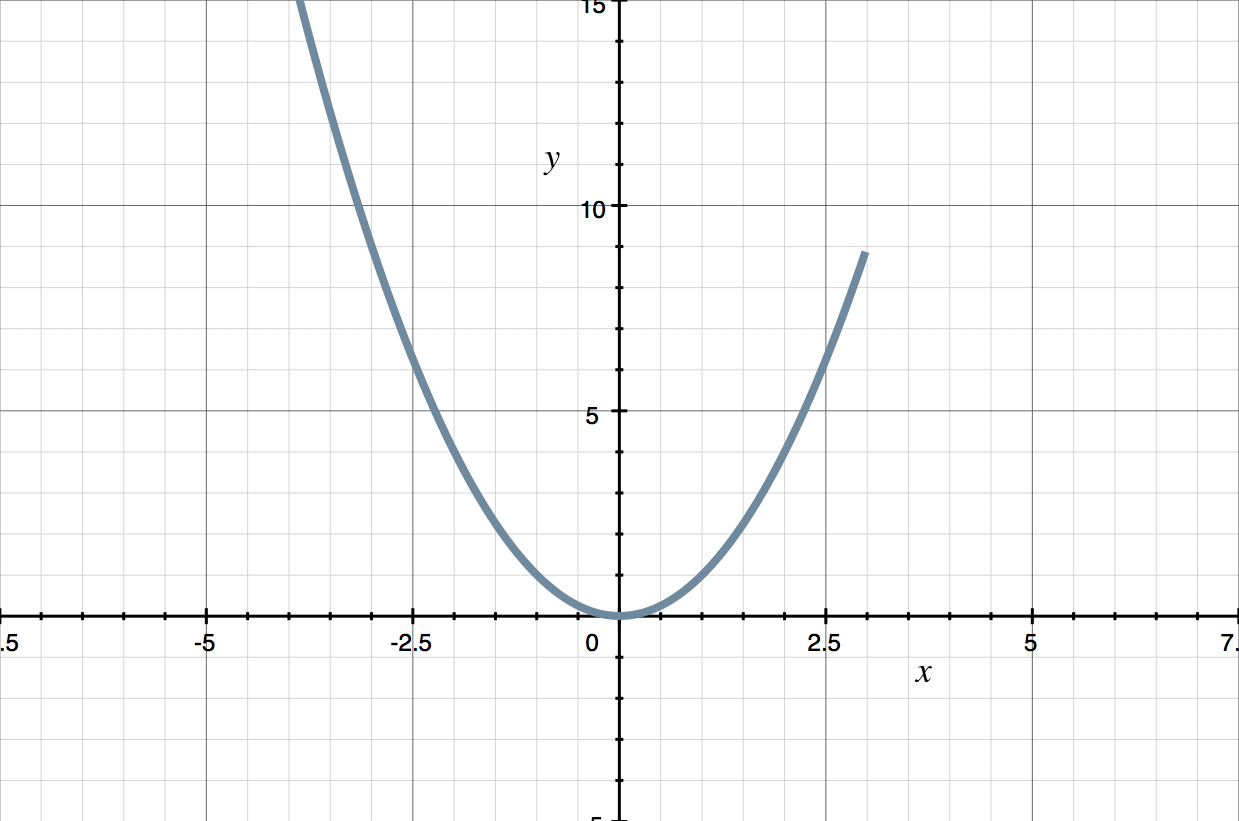
???f(x)=\begin{cases}x^2 & \quad x <3 \\8 & \quad x = 3\\2x+4 & \quad x > 3\end{cases}???
To graph a piecewise function, you graph each piece on its domain. Let’s start by graphing the piece with function ???x^2??? and domain ???x<3???, which is (part of) a parabola that opens upwards and has its vertex at the origin.
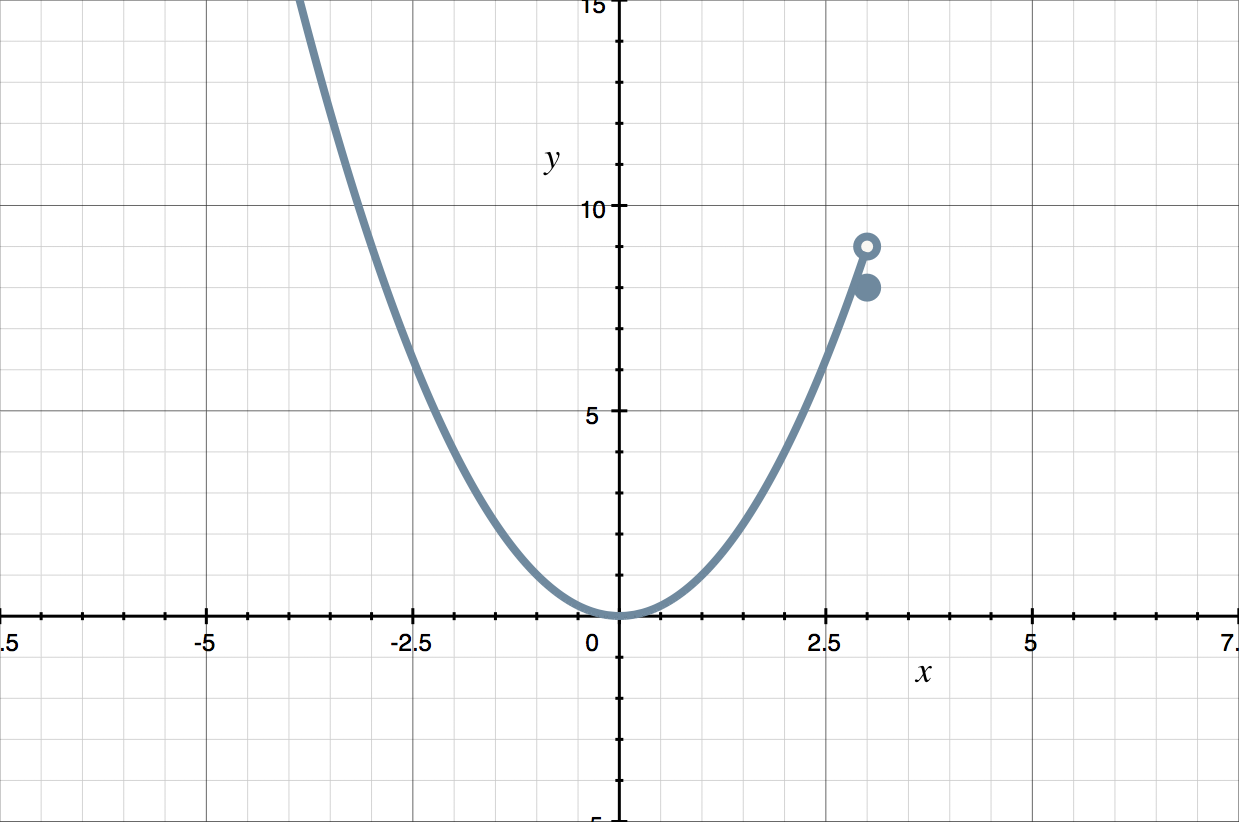
The domain of the next piece is just ???x=3???, and we’re given that ???f(3)=8???, so we’ll plot the point ???(3,8)???. For our graph to be the graph of a function, we can’t have two or more points with the same value of ???x???, so we’ll need to draw an open circle at the “right end” of the parabola, that is, at the point with ???x=3???, which has coordinates ???(3,3^2)???, or ???(3,9)???, to show that the point ???(3,9)??? isn’t a point of the graph of this piecewise function.
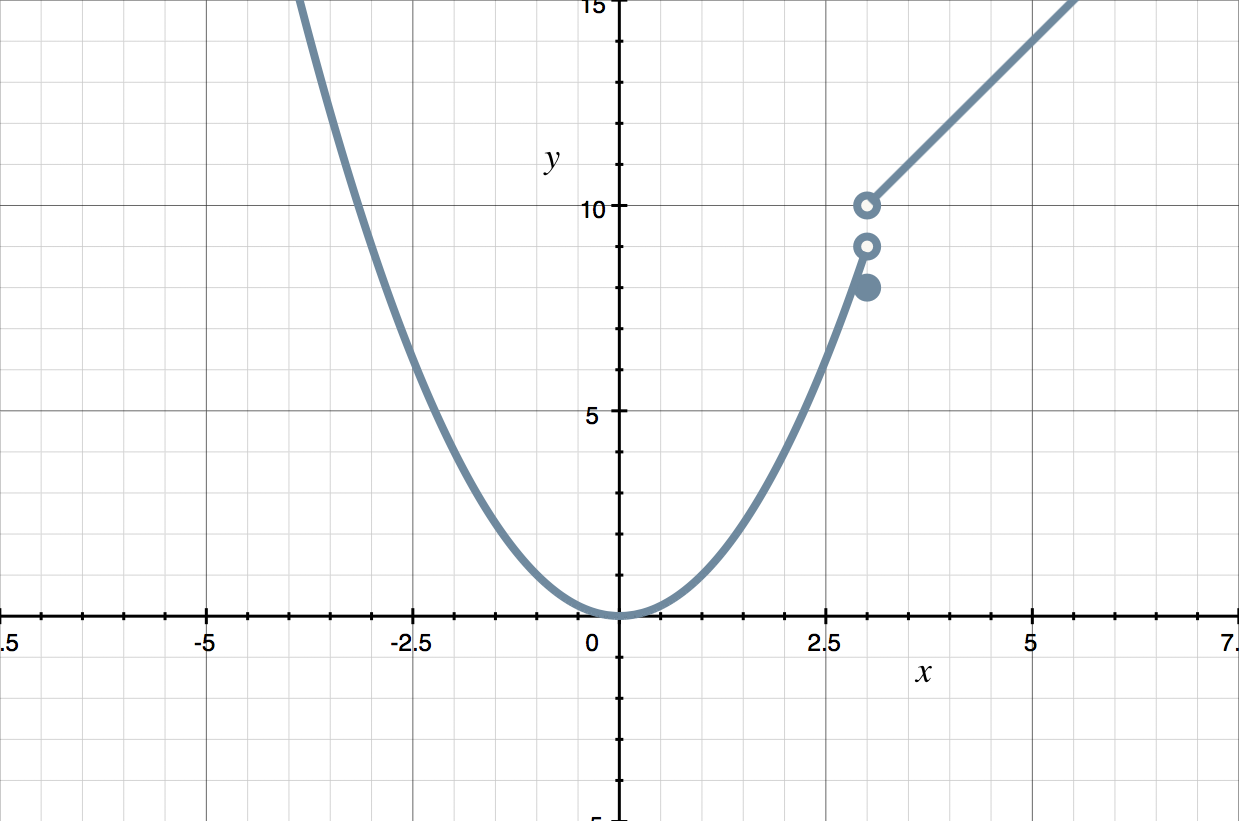
Next we need to graph the piece with function ???2x+4??? and domain ???x>3???, which is (part of) a line. When we graph this piece of the function, we’ll need to draw an open circle at the point of this line with ???x=3???, which has coordinates ???(3,2(3)+4)???, or ???(3,10)???, because it isn’t a point of the graph of this piecewise function.
You can also write the equation of a piecewise function when you’re given a graph.
How to break apart the pieces of the piecewise function
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Defining the piecewise function
Example
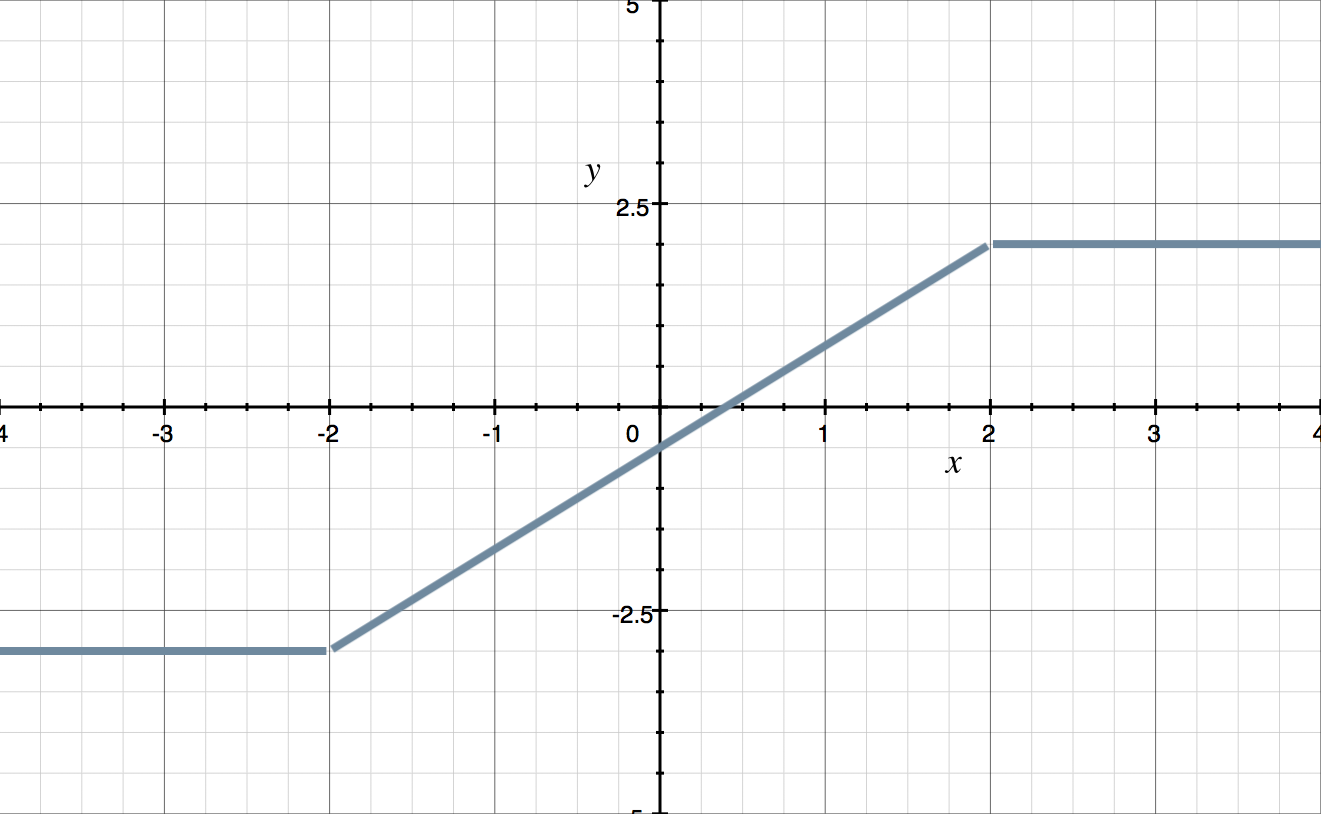
What is the definition of the piecewise function shown in the graph?
We’ll work on the graph from left to right. The horizontal line on the left has a ???y???-value of ???-3??? and includes all values of ???x??? in the interval ???x<-2??? (all real numbers ???x??? that are less than ???-2???). For this piece, we write ???-3??? for the function (the constant function whose value is ???-3???) and ???x<-2??? for its domain.
The slanted line has a slope of ???5/4??? and a ???y???-intercept of ???-1/2???. To see how to get the slope, notice that the points ???(-2,-3)??? and ???(2,2)??? are on this line, so
???y=\frac{5}{4}x-\frac{1}{2}???
For this piece, we write
???f(x)=\frac{5}{4}x-\frac{1}{2}???
for the function and ???-2\le x\le 2??? for its domain.
The horizontal line on the right has a ???y???-value of ???2??? and includes all values of ???x??? in the interval ???x>2???. For this piece, we write ???2??? for the function and ???x>2??? for its domain.
Putting the three pieces together, we define this piecewise function as follows:
???f(x) = \begin{cases} -3 & \quad x < -2 \\ \frac{5}{4}x-\frac12 & \quad -2 \leq x \leq 2\\ 2 & \quad x > 2 \end{cases}???
You might wonder how we decide which piece of this function gets the ???\le??? or ???\ge??? sign and which piece gets the ???<??? or ???>??? sign. The truth is that it doesn’t matter, as long as each ???x??? in the domain of the entire piecewise function is included in the domain of exactly one of its pieces - and, of course, that the function for that piece gives the correct value of ???f(x)???. You could write it this way, too:
???f(x)=\begin{cases}-3 & \quad x \leq -2 \\\frac{5}{4}x-\frac{1}{2} & \quad -2 < x <2\\2 & \quad x \geq 2\end{cases}???
But it could not be written as
???f(x)=\begin{cases}-3 & \quad x \leq -2 \\\frac{5}{4}x-\frac{1}{2} & \quad -2 \leq x \leq 2\\2 & \quad x \geq 2\end{cases}???
because here ???-2??? is included in the domains of two different pieces of the function, and so is ???2???.
Of course a piecewise function doesn’t need to have four pieces. It can have anywhere from two pieces to an infinite number of pieces. Usually, there are only two or three.
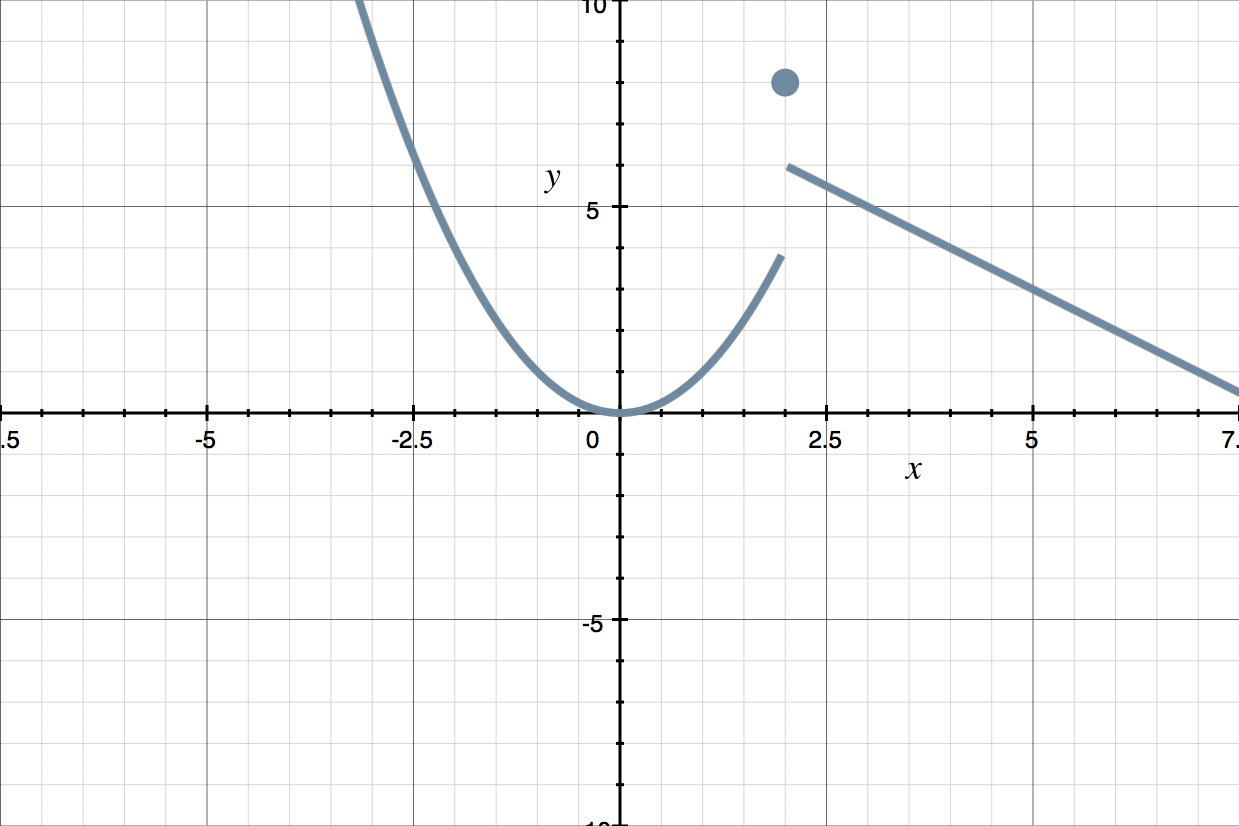
Example
What is the definition of the piecewise function shown in the graph.
Going from left to right, the first part of the graph is (part of) the parabola ???y=x^2???, which has its vertex at the origin. (To see that ???y=x^2??? is the equation of this parabola, note that it passes through the point ???(-2,4)??? and that ???4=(-2)^2???.) Thus the function for this piece is ???x^2???, and its domain is ???x<2???.
The second part of the graph is the point ???(2,8)???, so the function for this piece is ???8??? and its domain is ???x=2???.
The last part of the graph is part of the line ???y=-x+8???. To see this, we’ll first compute the slope from the points ???(8,0)??? and ???(2,6)???, both of which are on this line. Then we’ll use the slope and the point ???(8,0)??? to get the point-slope form of the equation of the line (and then use that to get the slope-intercept form). The slope is
???m =\frac{6-0}{2-8} =\frac{6}{-6} =-1???
The point-slope form of the equation of a line is
???y-y_1=m(x-x_1)???
Using ???(x_1,y_1)=(8,0)??? and the fact that ???m=-1???, we get
???y-0=-1(x-8)???
???y=-x+8???
Therefore, the function for the last piece is ???-x+8??? and its domain is ???x>2???.
Putting the three pieces together, we define this piecewise function as follows:
???f(x) = \begin{cases} x^2 & \quad\text{if}\quad x < 2\\ 8 & \quad\text{if}\quad x =2 \\ -x+8 & \quad\text{if}\quad x>2 \end{cases}???