Optimization problems with an open-top box
Steps for solving applied optimization problems
We’ve learned already how to use optimization to find the extrema of a function.
But we can use the optimization process for more than just sketching graphs of functions, or finding the highest and lowest points of the function’s graph.
Optimization in the real world
This same optimization process can be used in the real world. When the function we start with models some real-world scenario, then finding the function’s highest and lowest values means that we’re actually finding the maximum and minimum values in that situation.
For example, these are all things we can find by applying the optimization process to the real world:
the dimensions of a rectangle that maximize or minimize its area or perimeter
the maximum product or minimum sum of squares of two real numbers
the time at which velocity or acceleration is maximized or minimized
the dimensions that maximize or minimize the surface area or volume of a three-dimensional figure
the production or sales level that maximizes profit
This is only a tiny fraction of the many ways we can use optimization to find maxima and minima in the real world.
Solving optimization problems
When it comes to actually solving these problems, we’ll follow the same kinds of steps we took to solve optimization problems before.
Write an equation in one variable that represents the value we’re tying to maximize or minimize.
Take the derivative, set it equal to ???0??? to find critical points, and use the first derivative test to determine where the function is increasing and decreasing.
Based on the increasing/decreasing behavior of the function, identify the function’s maxima and minima.
Use the extrema to answer the question being asked.
With these steps in mind, let’s work through a typical applied optimization example. Keep in mind, there are many different kinds of applied optimization problems, but we solve all of them using this same set of steps.
An example of minimizing the surface area of an open-top box
Take the course
Want to learn more about Calculus 1? I have a step-by-step course for that. :)
Maximizing the volume of an open-top box
Example
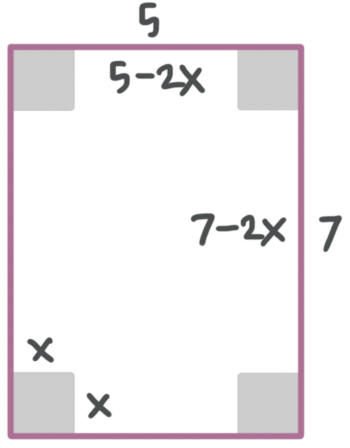
A ???5\times7??? piece of paper has squares of side-length ???x??? cut from each of its corners, such that folding up the sides will create a box with no top. Find the value of ???x??? that maximizes the volume of the open-top box.
First, we’ll sketch an image of the flat piece of paper.
The diagram shows the ???5\times7??? dimensions of the paper, and the ???x\times x??? square that was cut out of each corner. After cutting out the squares from the corners, the width of the open-top box will be ???5-2x???, and the length will be ???7-2x???.
We’re being asked to maximize the volume of a box, so we’ll use the formula for the volume of a box, and substitute in the length, width, and height of the open-top box.
???V=lwh???
???V=(7-2x)(5-2x)x???
???V=(35-14x-10x+4x^2)x???
???V=35x-14x^2-10x^2+4x^3???
???V=4x^3-24x^2+35x???
Now that we have the function we want to maximize, find the derivative.
???\frac{dV}{dx}=12x^2-48x+35???
Find critical points by setting the derivative equal to ???0???,
???12x^2-48x+35=0???
and then using the quadratic formula to solve for ???x???.
???x=\frac{48\pm \sqrt{2,304-1,680}}{24}???
???x=\frac{48\pm \sqrt{624}}{24}???
???x=\frac{12\pm \sqrt{39}}{6}???
So the critical points of the volume function are ???x\approx3.04??? and ???x\approx0.96???. But before we start testing critical points, we should always consider which of the critical points is even plausible.
Substitute ???x=3.04??? into the equations for the length and width of the open-top box.
???l=7-2x???
???l=7-2(3.04)???
???l=7-6.08???
???l=0.92???
and
???w=5-2x???
???w=5-2(3.04)???
???w=5-6.08???
???w=-1.08???
It’s nonsensical for the width of the box to be negative, so ???x=3.04??? can’t be a solution. If we try ???x=0.96??? in both the length and width equations, we get positive values for both, so ???x=0.96??? can be a potential solution.
So we’ll test ???0.96??? to make sure there’s a local maximum at that point. To test it, we’ll pick a value of ???x??? less than ???0.96???, and another greater than ???0.96???, and plug them into the derivative.
???\frac{dV}{dx}(0.5)=12(0.5)^2-48(0.5)+35???
???\frac{dV}{dx}(0.5)=14???
and
???\frac{dV}{dx}(2)=12(2)^2-48(2)+35???
???\frac{dV}{dx}(2)=-13???
Because the derivative is increasing (???14>0???) to the left of the critical point, and decreasing (???-13<0???) to the right of it, the function has a maximum at ???x=0.96???, and we can say that the volume of the open-top box is maximized when ???x=0.96???.