Mean Value Theorem for derivatives
What the Mean Value Theorem actually says
The Mean Value Theorem, in general, is a theorem that we use to prove that a function has a particular slope in an interval.
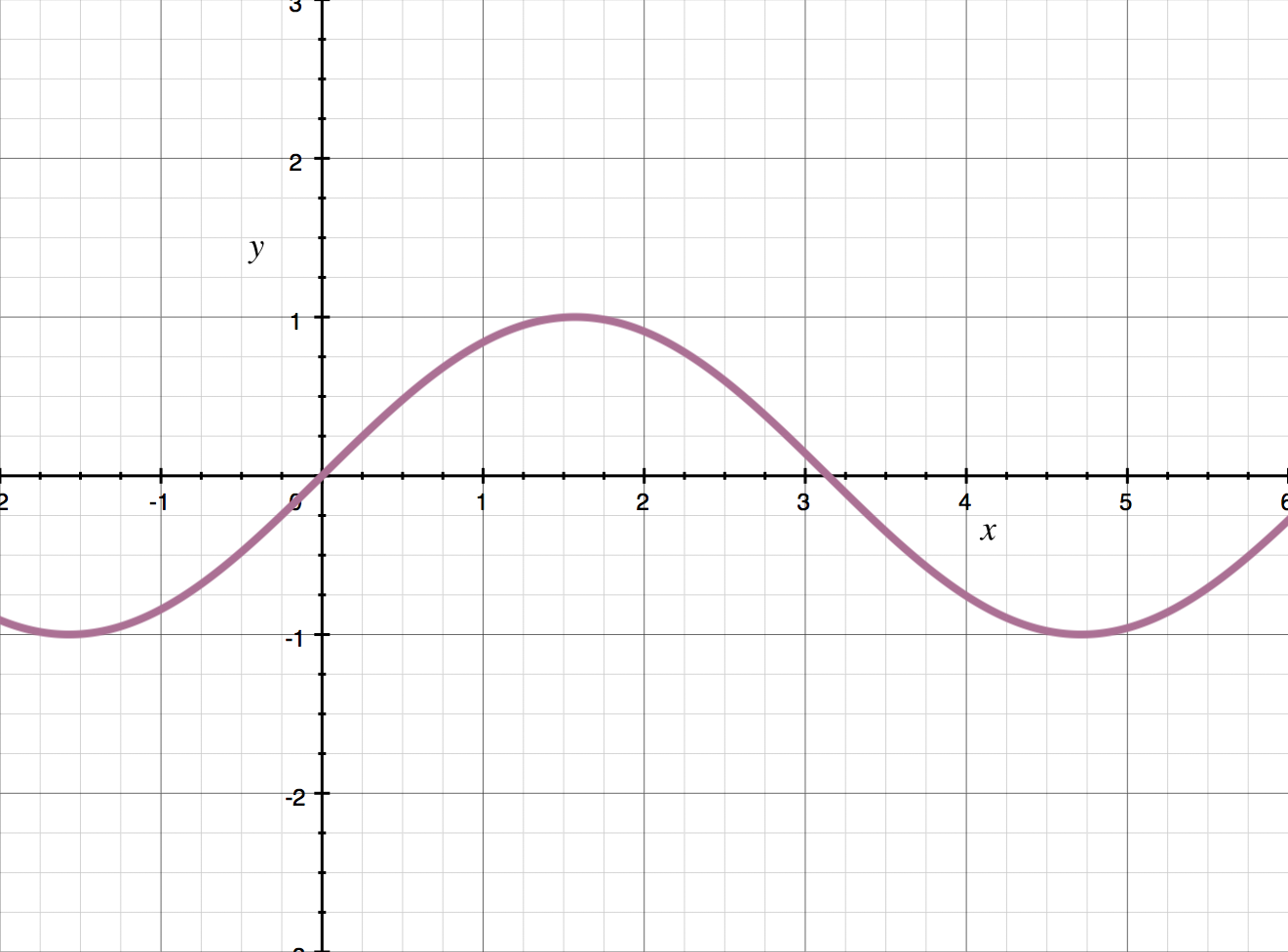
To break this down, let’s first think about some generic function. We’ll use ???y=\sin{x}???, whose graph looks like this:
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
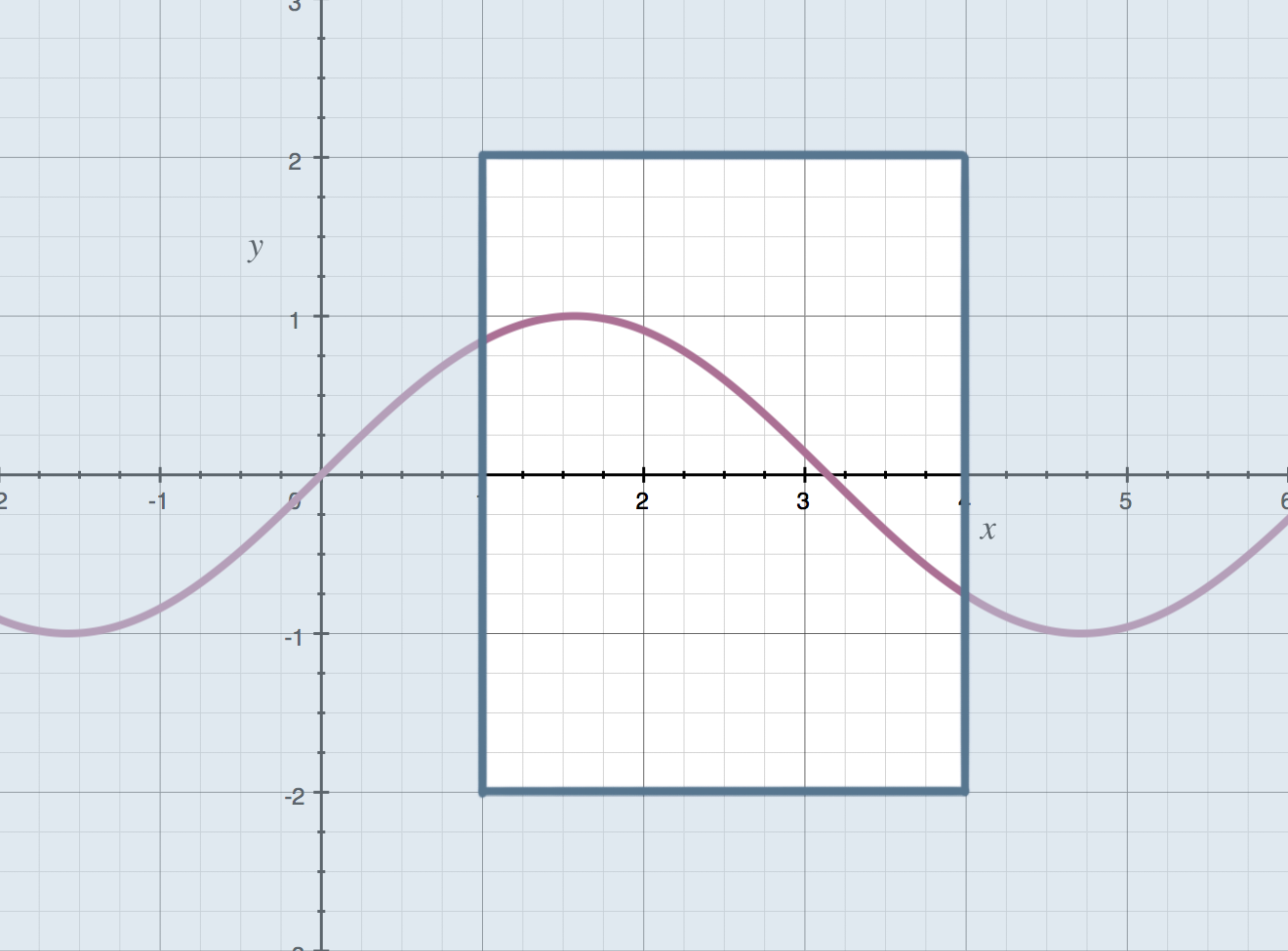
We can pick a closed interval, let’s say ???[1,4]???, and use it to bound the function. All we’re saying by picking the interval is that we’re only interested in what the function is doing inside that interval. Everything outside of that interval we can ignore.
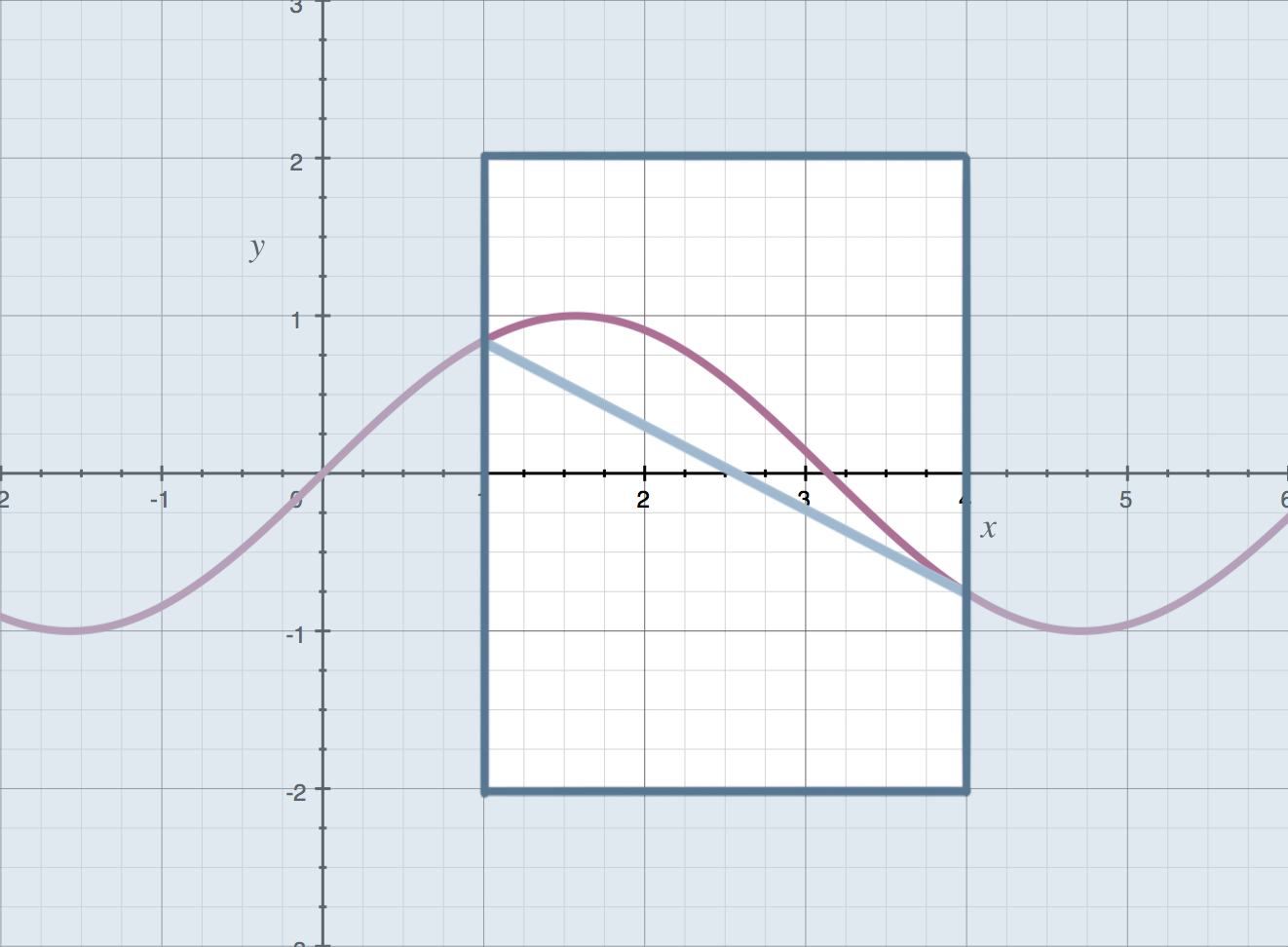
Once we’ve chosen an interval, look at the endpoints of the function at each edge of the interval, and connect them with a straight line.
The Mean Value Theorem tells us that, as long as the function is continuous (unbroken) and differentiable (smooth) everywhere inside the interval we’ve chosen, then there must be a line tangent to the curve somewhere in the interval, which is parallel to this line we’ve just drawn that connects the endpoints.
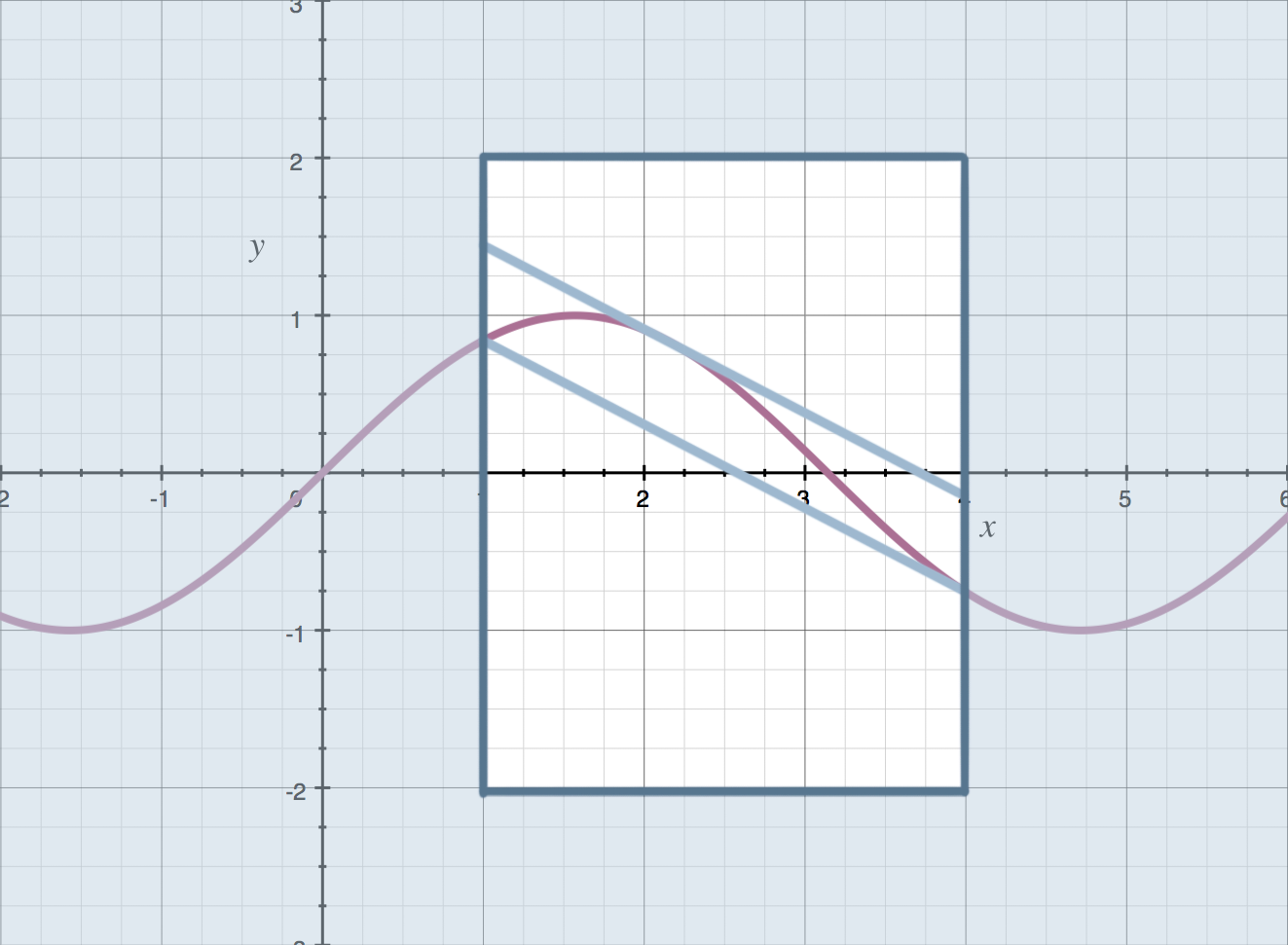
Here’s where that tangent line exists for this particular function we’ve been using:
Notice how it’s parallel to the line that connects the endpoints. This is what the Mean Value Theorem guarantees: a tangent line, somewhere inside the interval, that’s parallel to the line that connects the endpoints.
The point at which that tangent line intersects the curve (the point of tangency) will exist at ???x=c???. We call the interval ???[a,b]???, so ???c??? will fall between ???a??? and ???b???, ???a<c<b???. Then, mathematically, the Mean Value Theorem says
???f'(c)=\frac{f(b)-f(a)}{b-a}???
Practically, the consequence of the Mean Value Theorem is that the instantaneous rate of change at ???x=c??? will be equal to the average rate of change over the interval.
If we take that to the real world, it means we can say things like this:
If our average speed over the course of a long road trip is ???80??? km/h, then we must have been traveling at exactly ???80??? km/h at least at one moment during the road trip.
If the outdoor temperature on average throughout the morning increased by ???3^\circ??? per hour, then the hourly temperature increase must have been exactly ???3^\circ??? at some point during the morning.
If a child grew on average ???0.25??? inches per month over the course of a year, then their monthly growth rate must have been exactly ???0.25??? inches sometime during the year.
How to use the Mean Value Theorem to prove the existence of a tangent line with a particular slope in the interval
Take the course
Want to learn more about Calculus 1? I have a step-by-step course for that. :)
Applying the Mean Value Theorem to the real world
Example
We drive from Florida to California in exactly ???48??? hours, traveling a distance of ???3,000??? miles. Along the route we take, the speed limit is ???60??? mph. Use the Mean Value Theorem to prove that we were speeding at least at one point during the trip.
The Mean Value Theorem tells us that, as long as the function is continuous (unbroken) and differentiable (smooth) everywhere inside the interval we’ve chosen, then there must be a line tangent to the curve somewhere in the interval, which is parallel to this line we’ve just drawn that connects the endpoints.
Because the trip took ???48??? hours, we can set the interval at ???t=[0,48]???, and we can say that the function that models the trip is ???f(t)???. If we plug these values into the Mean Value Theorem, we get
???f'(c)=\frac{f(b)-f(a)}{b-a}???
???f'(c)=\frac{f(48)-f(0)}{48-0}???
???f'(c)=\frac{3,000-0}{48-0}???
???f'(c)=\frac{3,000}{48}???
???f'(c)=\frac{125}{2}???
???f'(c)=62.5???
This result tells us that, at least at one moment during the trip, we must have been traveling at ???62.5??? mph, which means we were speeding over the legal limit at some point along the way.