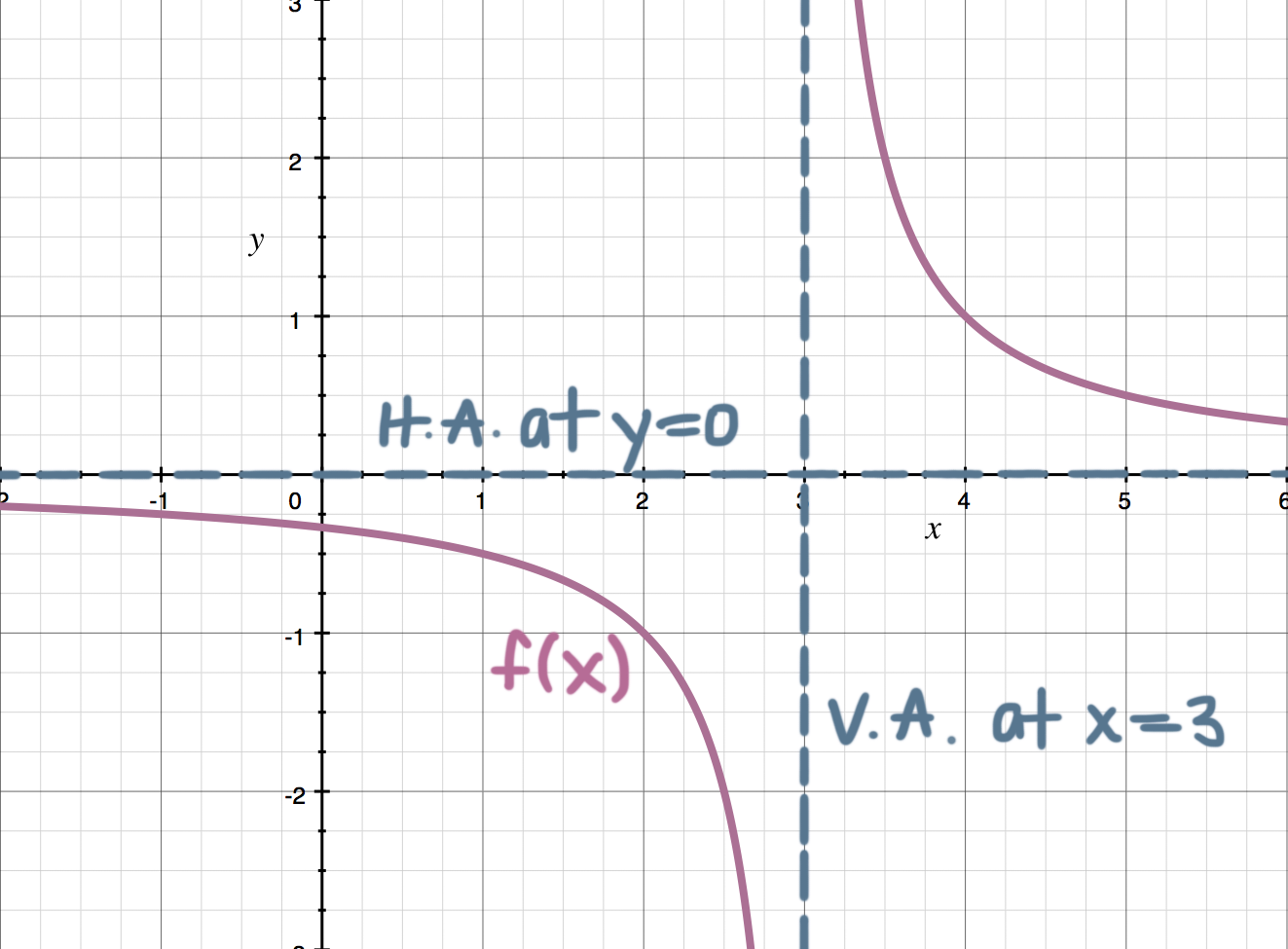Limits at infinity and horizontal asymptotes
What do we mean when we say "limits at infinity?"
“Limits at infinity” sounds a little mysterious, and it can be difficult to imagine the concept when we first hear this term. But let’s start by remembering that limits can be defined as the restrictions on the continuity of a function.
For the function ???f(x)=1/x???, ???x??? cannot equal ???0??? because the function doesn’t exist at that point. In this case, the limits would show that the function has an issue with continuity when ???x=0???. When we’re talking about continuity, we’re looking at values for which the function does not exist (it has a hole or an asymptote) or has a sudden break (where the function suddenly jumps without connection).
Looking at a function at infinity can be tricky, because we think about it like a number even though we don’t treat it the same as other numbers, because we’re not allowed to plug it into an equation directly. So when we’re talking about “limits at infinity”, we’re really just looking at the value of the function as ???x??? approaches positive or negative infinity.
If a function has a limit at infinity, it will appear to straighten out into a line as we move farther and farther away from the origin along the ???x???-axis. We can figure out the equation for this line by taking the limit of our equation as ???x??? approaches infinity. This line is called an asymptote.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Vertical and horizontal asymptotes
A function can have vertical asymptotes and/or horizontal asymptotes. A vertical asymptote occurs at a specific ???x???-value for all values of ???y??? (example ???x=4???). A horizontal asymptote occurs at a specific ???y???-value for all values of ???x??? (example ???y=9???).
In order to figure out if we have asymptotes, we will need to evaluate our function using limits. To figure out any potential horizontal asymptotes, we will use limits approaching infinity from the positive and negative direction. To figure out any potential vertical asymptotes, we will need to evaluate limits based on any continuity issues we might find in the denominator.
Walking through a video example of how to calculate the limit as x goes to infinity
Take the course
Want to learn more about Calculus 1? I have a step-by-step course for that. :)
Let's look at an example of how to find the limit at positive and negative infinity
Example
Evaluate both infinite limits.
???\lim_{x\to\pm\infty}\frac{1}{x-3}???
This function looks fairly simple, but it actually contains both a horizontal and a vertical asymptote (which means that the function is approaching ???\infty??? in both the ???x??? and ???y??? planes and in this case in both positive and negative directions).
Our first step is to take the limit of this function as ???x??? approaches ???+\infty??? and ???-\infty???. Let’s start with ???+\infty???.
???\lim_{x \to +\infty} \frac{1}{x-3}???
To solve, we substitute our limit (in this case ???+\infty???) for ???x???.
???\frac{1}{\infty-3}???
At this point, we need to think logically. We have a fraction with an extremely large denominator, and a numerator that is, in comparison, incredibly small. In the world of math, we consider any fraction with a small number on top and infinity on the bottom to be equal to zero, so
???\frac{1}{\infty-3}=0???
???\lim_{x \to +\infty} \frac{1}{x-3}= 0???
This means that as ???x??? approaches ???\infty???, the function has a horizontal asymptote at ???y=0???.
Next let’s deal with the limit as ???x??? approaches ???-\infty???.
???\lim_{x \to -\infty} \frac{1}{x-3}???
???\frac{1}{-\infty-3}=0???
???\lim_{x \to -\infty} \frac{1}{x-3}= 0???
This means that we have a horizontal asymptote at ???y=0??? as ???x??? approaches ???-\infty???.
"limit at infinity" means finding the limit of the function as you approach positive or negative infinity
We just found the function’s limits at infinity, because we were looking at the value of the function as ???x??? was approaching ???\pm\infty???. But we can also look at the function’s infinite limits, which occur at specific values of ???x??? where the function’s value is ???\pm\infty???. The difference between “limits at infinity” and “infinite limits” is discussed in greater detail at the beginning of the next section.
In the meantime, let’s use this same example to look for vertical asymptotes where the function has infinite limits.
Example (continued)
To test for potential vertical asymptotes, we set the denominator equal to ???0??? and solve for ???x???.
???x-3=0???
???x=3???
This means we have a vertical asymptote at ???x=3???.
To confirm our conclusion, we can take the limit of our original function as it approaches ???3??? from the positive and negative direction (if we did, in fact, find a vertical asymptote, our limits should be ???+\infty??? and/or ???-\infty???).
???\lim_{x \to 3^+} \frac{1}{x-3}???
We can’t solve for the limit by substituting ???3??? in for ???x??? directly, because we’ll get ???1/0???. Instead, let’s test the function at ???3.00001??? or ???3.00000000001???, or an even smaller increment, to see how the function behaves around ???3???. Plugging those values into our function one at a time, we notice that the value of the function gets larger and larger. This means that, as ???x??? approaches ???3??? from the right, the function is approaching ???+\infty???.
???\lim_{x \to 3^+} \frac{1}{x-3}= +\infty???
Let’s look at the limit as ???x??? approaches ???3??? from the left.
???\lim_{x \to 3^-} \frac{1}{x-3}???
In this case, we need to use ???2.9999??? or ???2.999999999??? or a number even closer to ???3???. Plugging these values into our function, we see that the value of the function becomes an increasingly large negative number, which means that the function is approaching ???-\infty???.
???\lim_{x \to 3^-} \frac{1}{x-3}= -\infty???
We can always use this information to sketch a graph of the function and label its vertical and horizontal asymptotes.