Intersecting tangents and secants of circles, intersecting inside the circle and outside the circle
Different ways in which tangents and secants of circles intersect each other
In this lesson we’ll look at the relationships formed from intersecting tangents and secants in circles.
Secant
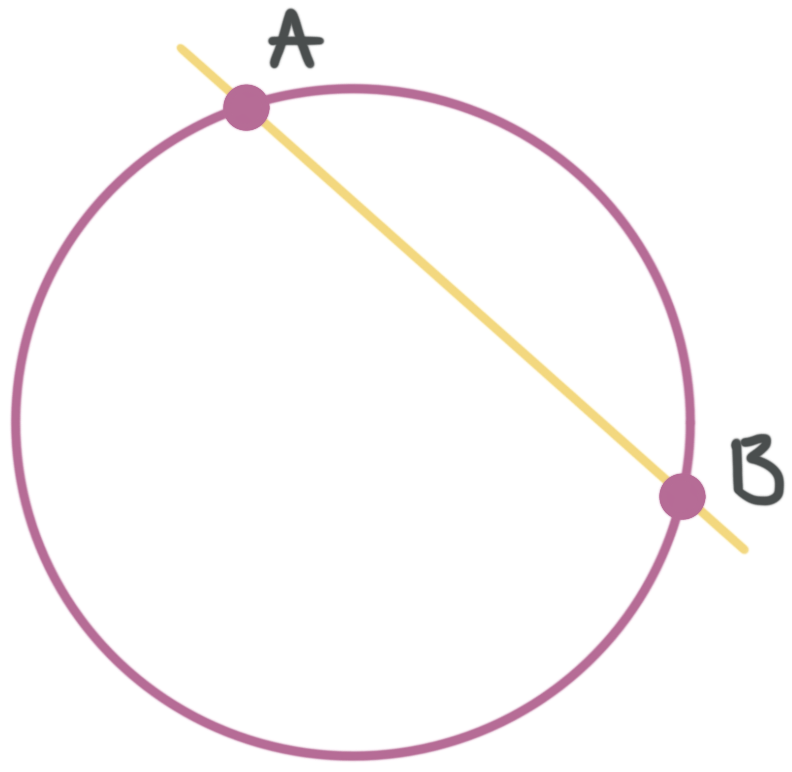
The secant of a circle is a line or line segment that intersects the circle at two points. ???\overline{AB}??? is a secant of this circle.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Intersecting secants theorem
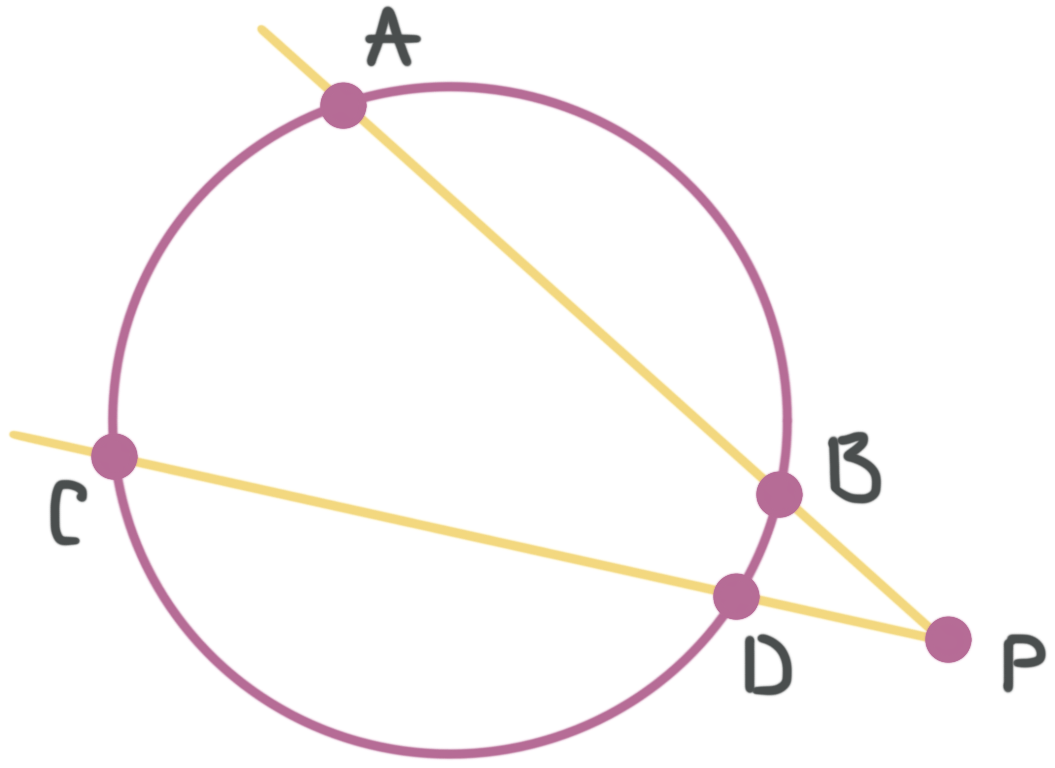
There’s a special relationship between two secants that intersect outside of a circle. The length outside the circle, multiplied by the length of the whole secant is equal to the outside length of the other secant multiplied by the whole length of the other secant. In the following circle, the secants ???\overline{AP}??? and ???\overline{CP}??? intersect at point ???P???,
so
???BP\cdot AP=DP\cdot CP???
Tangents
The tangent of a circle is a line or line segment that intersects a circle at only one point. Line ???AB??? is a tangent of this circle.
Intersecting tangent-secant theorem
There is also a special relationship between a tangent and a secant that intersect outside of a circle. The length of the outside portion of the tangent, multiplied by the length of the whole secant, is equal to the squared length of the tangent. Tangent line ???AP??? and secant ???\overline{DP}??? intersect at point ???P???,
so
???AP^2=DP\cdot BP???
Multiple examples of tangents and secants of circles, which intersect each other inside the circle or outside the circle
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Finding the length of a piece of the secant
Example
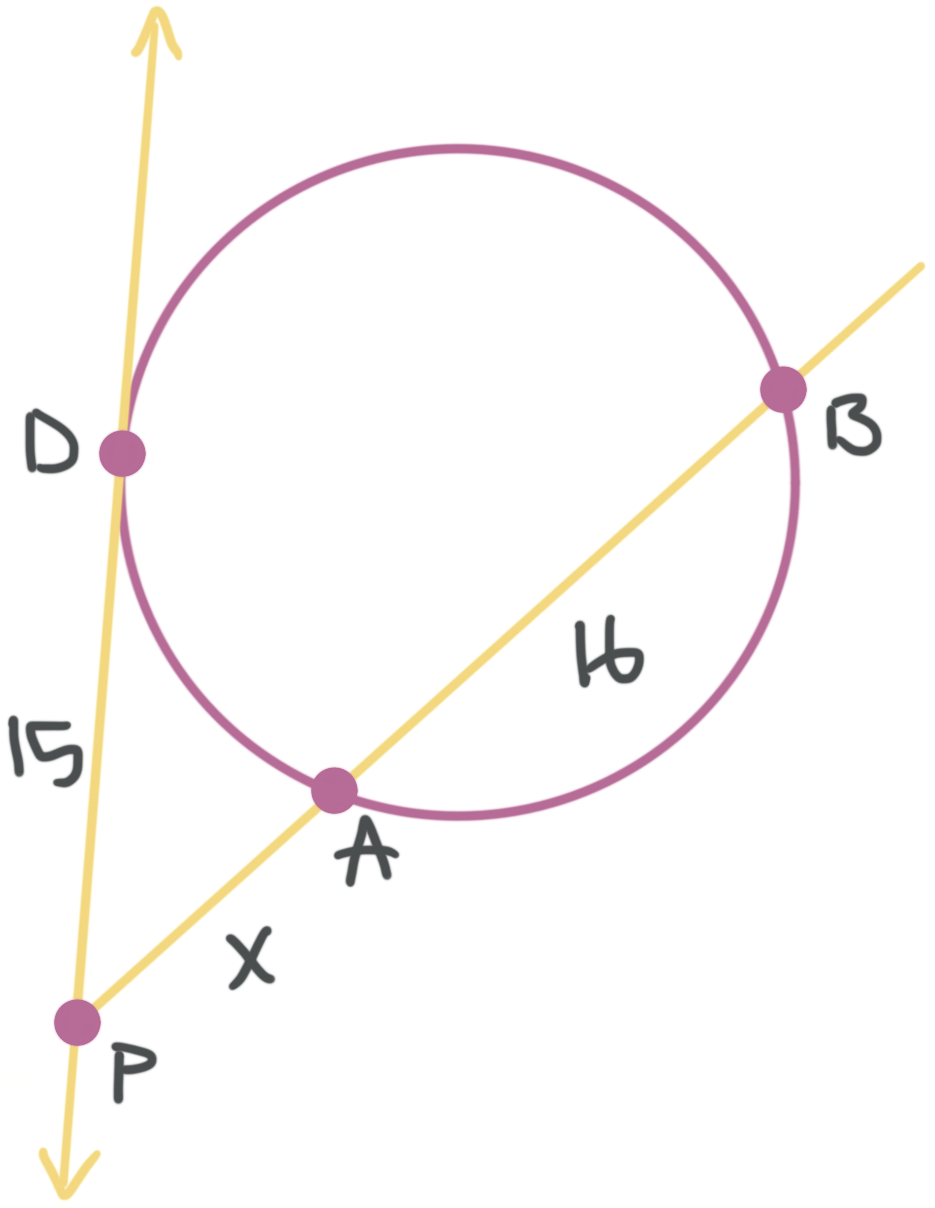
Solve for the value of ???x??? in the figure, assuming ???DP??? is a tangent.
Because there’s a secant intersecting with a tangent, we can follow the formula and plug in the values from the figure.
???\text{outside}\cdot \text{whole} = \text{tangent}^2???
???x(x+16)={{15}^{2}}???
???{{x}^{2}}+16x=225???
???{{x}^{2}}+16x-225=0???
???(x+25)(x-9)=0???
???x=-25??? or ???x=9???
A line segment can’t have a negative length, so rule out ???x=-25??? and conclude that ???x=9???.
Let’s do one more problem.
The length of the outside portion of the tangent, multiplied by the length of the whole secant, is equal to the squared length of the tangent.
Finding the length of the part of the secant inside the circle
Example
Given the lengths in the figure, solve for ???x???.
Because there are two secants intersecting, we can follow the formula and plug in the values from the figure.
???\text{outside}\cdot \text{whole}=\text{outside}\cdot \text{whole}???
???5(x-6+5)=4(x-3+4)???
???5(x-1)=4(x+1)???
???5x-5=4x+4???
???x-5=4???
???x=9???