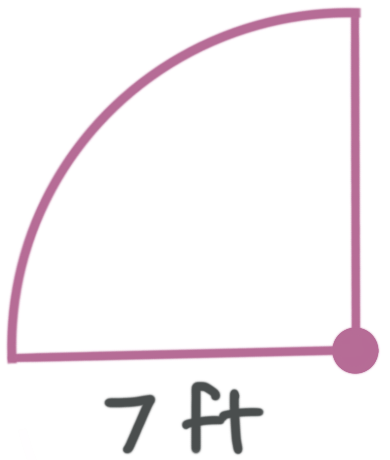Finding the circumference of a circle
Formula for the circumference of a circle
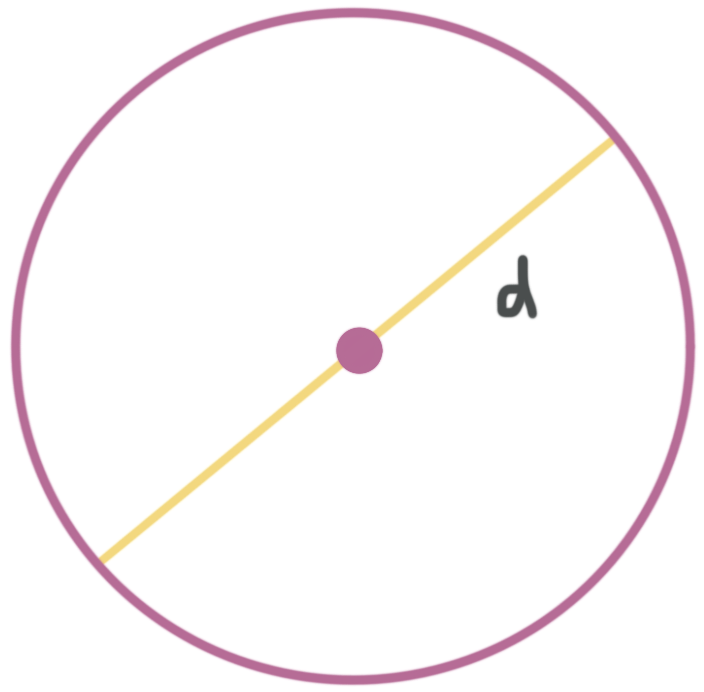
Remember that the radius of a circle is the length from its center to a point on its circumference,
and that the diameter is a special chord that passes through the center of the circle. The diameter is always made of two radii, such that ???d=2r???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
And ???\pi??? is a special number, ???\pi \approx 3.14???, that describes the relationship between a circle’s circumference and the length of its diameter.
Circumference of a circle
The circumference of a circle is the distance around the circle (its perimeter) and it’s equal to ???2???, multiplied by ???\pi??? and the radius, or just ???\pi??? times the diameter.
???C=2\pi r???
???C=\pi d???
Finding circumference, given the radius or diameter
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Finding circumference given the diameter of the circle
Example
What is the circumference of a circle with a diameter of ???10\text{ in}????
The formula for the circumference of a circle when we know a circle’s diameter is ???C=\pi d???. We know the diameter of the circle is ???10\text{ in}??? so when we plug this in to the formula we get
???C=\pi \cdot 10???
???C=10\pi \text{ in}???
???C\approx 10(3.14)\text{ in}???
???C\approx 31.4\text{ in}???
Sometimes you could be asked to find the circumference of part of a circle.
The circumference of a circle is the distance around the circle,
Finding the circumference of a quarter circle
Example
To the nearest hundredth, what is the circumference of the arc of this quarter circle?
The formula for circumference when you know the radius is ???C=2\pi r???, and we know the radius is ???7??? feet, so the circumference is
???C=2\pi (7)\text{ ft}???
???C=14\pi \text{ ft}???
This is the full circumference, so we need to divide this circumference by ???4??? to find the length of the arc.
???\frac{C}{4}=\frac{14\pi \text{ ft}}{4}=3.5\pi \text{ ft}???
Notice if we had been asked to find the perimeter of the figure, we would have needed to add the lengths of the radii to this portion of the circumference. The perimeter would be
???P\approx 10.99\text{ ft} + 7 \text{ ft}+7\text{ ft}???
???P\approx 24.99\text{ ft}???